
【題目】已知函數(shù)f(x)=aln x-bx2 , a,b∈R.
(1)若f(x)在x=1處與直線y=- ![]() 相切,求a,b的值;
相切,求a,b的值;
(2)在(1)的條件下,求f(x)在 ![]() 上的最大值;
上的最大值;
(3)若不等式f(x)≥x對(duì)所有的b∈(-∞,0],x∈(e,e2]都成立,求a的取值范圍.
【答案】
(1)解:f′(x)= ![]() -2bx.由函數(shù)f(x)在x=1處與直線y=-
-2bx.由函數(shù)f(x)在x=1處與直線y=- ![]() 相切,
相切,
得  即
即 
解得 ![]()
(2)解:由(1)得f(x)=ln x- ![]() x2 , 定義域?yàn)?0,+∞).
x2 , 定義域?yàn)?0,+∞).
此時(shí),f′(x)= ![]() -x=
-x= ![]() ,令f′(x)>0,解得0<x<1,令f′(x)<0,解得x>1.
,令f′(x)>0,解得0<x<1,令f′(x)<0,解得x>1.
所以f′(x)在 ![]() 上單調(diào)遞增,在(1,e)上單調(diào)遞減,
上單調(diào)遞增,在(1,e)上單調(diào)遞減,
所以f(x)在 ![]() 上的最大值為f(1)=-
上的最大值為f(1)=- ![]() .
.
(3)解:若不等式f(x)≥x對(duì)所有的b∈(-∞,0],x∈(e,e2]都成立,
即aln x-bx2≥x對(duì)所有的b∈(-∞,0],x∈(e,e2]都成立,
即aln x-x≥bx2對(duì)所有的b∈(-∞,0],x∈(e,e2]都成立,
即aln x-x≥0對(duì)x∈(e,e2]恒成立,
即a≥ ![]() 對(duì)x∈(e,e2]恒成立,
對(duì)x∈(e,e2]恒成立,
即a大于等于 ![]() 在區(qū)間(e,e2]上的最大值.
在區(qū)間(e,e2]上的最大值.
令h(x)= ![]() ,則h′(x)=
,則h′(x)= ![]() ,當(dāng)x∈(e,e2)時(shí),h′(x)>0,h(x)單調(diào)遞增,
,當(dāng)x∈(e,e2)時(shí),h′(x)>0,h(x)單調(diào)遞增,
所以h(x)= ![]() ,x∈(e,e2]的最大值為h(e2)=
,x∈(e,e2]的最大值為h(e2)= ![]() ,即a≥
,即a≥ ![]() .
.
所以a的取值范圍為 ![]() .
.
【解析】本題考查導(dǎo)數(shù)的運(yùn)用:求切線的斜率和單調(diào)區(qū)間、極值和最值,考查不等式的恒成立問(wèn)題注意運(yùn)用參數(shù)分離和轉(zhuǎn)化為求函數(shù)的最值問(wèn)題,屬于中檔題和易錯(cuò)題.導(dǎo)數(shù)和函數(shù)的單調(diào)性的關(guān)系:
(1)若f′(x)>0在(a,b)上恒成立,則f(x)在(a,b)上是增函數(shù),f′(x)>0的解集與定義域的交集的對(duì)應(yīng)區(qū)間為增區(qū)間;
(2)若f′(x)<0在(a,b)上恒成立,則f(x)在(a,b)上是減函數(shù),f′(x)<0的解集與定義域的交集的對(duì)應(yīng)區(qū)間為減區(qū)間.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知集合A={x|x<1},B={x|3x<1},則( )
A.A∩B={x|x<0}
B.A∪B=R
C.A∪B={x|x>1}
D.A∩B=
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖, ![]() 為半圓
為半圓 ![]() 的直徑,點(diǎn)
的直徑,點(diǎn) ![]() 是半圓弧上的兩點(diǎn),
是半圓弧上的兩點(diǎn), ![]() ,
, ![]() .曲線
.曲線 ![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn) ![]() ,且曲線
,且曲線 ![]() 上任意點(diǎn)
上任意點(diǎn) ![]() 滿足:
滿足: ![]() 為定值.
為定值.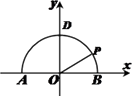
(Ⅰ)求曲線 ![]() 的方程;
的方程;
(Ⅱ)設(shè)過(guò)點(diǎn) ![]() 的直線
的直線 ![]() 與曲線
與曲線 ![]() 交于不同的兩點(diǎn)
交于不同的兩點(diǎn) ![]() ,求
,求 ![]() 面積最大時(shí)的直線
面積最大時(shí)的直線 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】近年來(lái)隨著我國(guó)在教育利研上的投入不斷加大,科學(xué)技術(shù)得到迅猛發(fā)展,國(guó)內(nèi)企業(yè)的國(guó)際競(jìng)爭(zhēng)力得到大幅提升.伴隨著國(guó)內(nèi)市場(chǎng)增速放緩,國(guó)內(nèi)確實(shí)力企業(yè)紛紛進(jìn)行海外布局,第二輪企業(yè)出海潮到來(lái),如在智能手機(jī)行業(yè),國(guó)產(chǎn)品牌已在趕超國(guó)外巨頭,某品牌手機(jī)公司一直默默拓展海外市場(chǎng),在海外共設(shè)30多個(gè)分支機(jī)構(gòu),需要國(guó)內(nèi)公司外派大量70后、80后中青年員工.該企業(yè)為了解這兩個(gè)年齡層員工是否愿意被外派上作的態(tài)度,按分層抽樣的方式從70后利80后的員工中隨機(jī)調(diào)查了100位,得到數(shù)據(jù)如下表:
愿意被外派 | 不愿意被外派 | 合計(jì) | |
70后 | 20 | 20 | 40 |
80后 | 40 | 20 | 60 |
合計(jì) | 60 | 40 | 100 |
參考數(shù)據(jù):
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(參考公式: ![]() ,其中
,其中 ![]() )
)
(1)根據(jù)查的數(shù)據(jù),是否有 ![]() 的把握認(rèn)為“是否愿意被外派與年齡有關(guān)”,并說(shuō)明理由;
的把握認(rèn)為“是否愿意被外派與年齡有關(guān)”,并說(shuō)明理由;
(2)該公司參觀駐海外分支機(jī)構(gòu)的交流體驗(yàn)活動(dòng),擬安排4名參與調(diào)查的70后員工參加,70后的員工中有愿意被外派的3人和不愿意被外派的3人報(bào)名參加,現(xiàn)采用隨機(jī)抽樣方法從報(bào)名的員工中選4人,求選到愿意被外派人數(shù)不少于不愿意被外派人數(shù)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知曲線 ![]() 的參數(shù)方程為
的參數(shù)方程為 ![]() (
( ![]() 為參數(shù)),直線
為參數(shù)),直線 ![]() 的參數(shù)方程為
的參數(shù)方程為 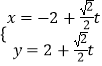 (
( ![]() 為參數(shù)).
為參數(shù)).
(Ⅰ)求曲線 ![]() 和直線
和直線 ![]() 的普通方程;
的普通方程;
(Ⅱ)若點(diǎn) ![]() 為曲線
為曲線 ![]() 上一點(diǎn),求點(diǎn)
上一點(diǎn),求點(diǎn) ![]() 到直線
到直線 ![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知圓 ![]() 與直線
與直線 ![]() 相切.
相切.
(1)若直線 ![]() 與圓
與圓 ![]() 交于
交于 ![]() 兩點(diǎn),求
兩點(diǎn),求 ![]() ;
;
(2)設(shè)圓 ![]() 與
與 ![]() 軸的負(fù)半軸的交點(diǎn)為
軸的負(fù)半軸的交點(diǎn)為 ![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn) ![]() 作兩條斜率分別為
作兩條斜率分別為 ![]() 的直線交圓
的直線交圓 ![]() 于
于 ![]() 兩點(diǎn),且
兩點(diǎn),且 ![]() ,試證明直線
,試證明直線 ![]() 恒過(guò)一定點(diǎn),并求出該定點(diǎn)的坐標(biāo).
恒過(guò)一定點(diǎn),并求出該定點(diǎn)的坐標(biāo).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com