
【題目】已知直線C1 ![]() (t為參數),C2
(t為參數),C2 ![]() (θ為參數),
(θ為參數),
(Ⅰ)當α= ![]() 時,求C1與C2的交點坐標;
時,求C1與C2的交點坐標;
(Ⅱ)過坐標原點O做C1的垂線,垂足為A,P為OA中點,當α變化時,求P點的軌跡的參數方程,并指出它是什么曲線.
【答案】解:(Ⅰ)當α= ![]() 時,C1的普通方程為
時,C1的普通方程為 ![]() ,C2的普通方程為x2+y2=1.
,C2的普通方程為x2+y2=1.
聯立方程組 ![]() ,
,
解得C1與C2的交點為(1,0) ![]() .
.
(Ⅱ)C1的普通方程為xsinα-ycosα-sinα=0①.
則OA的方程為xcosα+ysinα=0②,
聯立①②可得x=sin2α,y=-cosαsinα;
A點坐標為(sin2α,-cosαsinα),
故當α變化時,P點軌跡的參數方程為: 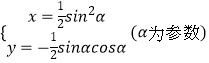
P點軌跡的普通方程 ![]() .
.
故P點軌跡是圓心為 ![]() ,半徑為
,半徑為 ![]() 的圓
的圓
【解析】(1)根據題意結合已知條件求出直線的方程再聯立直線與圓的方程即可求出交點的坐標。(2)首先聯立兩個方程求出點A的坐標由角的變化得出點P的參數方程再根據極坐標和直角坐標的互化關系得出圓的標準方程進而求出圓心坐標以及半徑。


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD為正方形,PA⊥底面ABCD,AD=AP,E為棱PD中點. 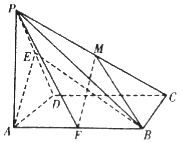
(1)求證:PD⊥平面ABE;
(2)若F為AB中點, ![]() ,試確定λ的值,使二面角P﹣FM﹣B的余弦值為-
,試確定λ的值,使二面角P﹣FM﹣B的余弦值為- ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數 ![]() (
( ![]() 為常數,e=2.71828……是自然對數的底數).
為常數,e=2.71828……是自然對數的底數).
(1)當 ![]() 時,求函數
時,求函數 ![]() 的單調區間;
的單調區間;
(2)若函數 ![]() 在
在 ![]() 內存在兩個極值點,求
內存在兩個極值點,求 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的一系列對應值如下表:
的一系列對應值如下表:
|
|
|
|
|
|
|
|
| -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(1)根據表格提供的數據畫出函數![]() 的圖像并求出函數解析式;
的圖像并求出函數解析式;
(2)根據(1)的結果,若函數![]() 的周期為
的周期為![]() ,當
,當![]() 時,方程
時,方程![]() 恰有兩個不同的解,求實數
恰有兩個不同的解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我們國家正處于老齡化社會中,老有所依也是政府的民生工程.某市共有戶籍人口400萬,其中老人(年齡60歲及以上)人數約有66萬,為了解老人們的健康狀況,政府從 老人中隨機抽取600人并委托醫療機構免費為他們進行健康評估,健康狀況共分為不能 自理、不健康尚能自理、基本健康、健康四個等級,并以80歲為界限分成兩個群體進行 統計,樣本分布被制作成如圖表: 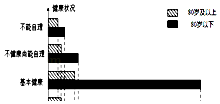
(1)若采取分層抽樣的方法再從樣本中的不能自理的老人中抽取16人進一步了解他們的生活狀況,則兩個群體中各應抽取多少人?
(2)估算該市80歲及以上長者占全市戶籍人口的百分比;
(3)據統計該市大約有五分之一的戶籍老人無固定收入,政府計劃為這部分老人每月發 放生活補貼,標準如下:①80歲及以上長者每人每月發放生活補貼200元;②80歲以下 老人每人每月發放生活補貼120元;③不能自理的老人每人每月額外發放生活補貼100 元.試估計政府執行此計劃的年度預算.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() ,記函數
,記函數![]() 的定義域為
的定義域為![]() .
.
(1)求函數![]() 的定義域
的定義域![]() ;
;
(2)若函數![]() 的最大值為2,求
的最大值為2,求![]() 的值;
的值;
(3)若對于![]() 內的任意實數
內的任意實數![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}中,a1=1,a3=9,且an=an﹣1+λn﹣1(n≥2).
(1)求λ的值及數列{an}的通項公式;
(2)設 ![]() ,且數列{bn}的前n項和為Sn , 求S2n .
,且數列{bn}的前n項和為Sn , 求S2n .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com