
【題目】已知向量 ![]() =(﹣2sin(π﹣x),cosx),
=(﹣2sin(π﹣x),cosx), ![]() =(
=( ![]() cosx,2sin(
cosx,2sin( ![]() ﹣x)),函數f(x)=1﹣
﹣x)),函數f(x)=1﹣ ![]()
![]() .
.
(1)若x∈[0, ![]() ],求函數f(x)的值域;
],求函數f(x)的值域;
(2)當x∈[0,π]時,求f(x)的單調遞增區間.
【答案】
(1)解:由題意: ![]() =(﹣2sin(π﹣x),cosx),
=(﹣2sin(π﹣x),cosx), ![]() =(
=( ![]() cosx,2sin(
cosx,2sin( ![]() ﹣x)),
﹣x)),
函數f(x)=1﹣ ![]()
![]()
=1+2 ![]() cosxsin(π﹣x)﹣2cosxsin(
cosxsin(π﹣x)﹣2cosxsin( ![]() ﹣x)
﹣x)
=1+2 ![]() sinxcosx﹣2cos2x
sinxcosx﹣2cos2x
=1+ ![]() sin2x﹣1﹣cos2x
sin2x﹣1﹣cos2x
= ![]() sin2x﹣cos2x
sin2x﹣cos2x
=2sin(2x﹣ ![]() ),
),
當x∈[0, ![]() ]時,2x-
]時,2x- ![]() ∈[-
∈[- ![]() ,
, ![]() ],
],
當x=- ![]() 時,f(x)取值最小值為﹣1,
時,f(x)取值最小值為﹣1,
當x= ![]() 時,f(x)取得最大值為2,
時,f(x)取得最大值為2,
所以函數f(x)的值域為[﹣1,2]
(2)解:由(1)可得f(x)=2sin(2x﹣ ![]() ),
),
由正弦函數圖象及性質可知:單調遞增區間為[ ![]() ,
, ![]() ](k∈Z).
](k∈Z).
即 ![]() ≤
≤ ![]() (k∈Z).
(k∈Z).
解得: ![]() (k∈Z).
(k∈Z).
又∵x∈[0,π]
當k=0時,可得: ![]() .
.
當k=1時,可得: ![]() .
.
∴f(x)的單調遞增區間為[0, ![]() ]和[
]和[ ![]() ,π]
,π]
【解析】(1)利用向量的乘積運算求出f(x)的解析式,將函數化為y=Asin(ωx+φ)的形式,在求解x∈[0, ![]() ],函數f(x)的最值,即可得值域.(2)當x∈[0,π]時,求出內層函數的范圍,放到正弦函數的增區間上,解不等式得函數的單調遞增區間;求f(x)的單調遞增區間.
],函數f(x)的最值,即可得值域.(2)當x∈[0,π]時,求出內層函數的范圍,放到正弦函數的增區間上,解不等式得函數的單調遞增區間;求f(x)的單調遞增區間.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知圓O外有一點P,作圓O的切線PM,M為切點,過PM的中點N,作割線NAB,交圓于A,B兩點,連接PA并延長,交圓O于點C,連續PB交圓O于點D,若MC=BC. 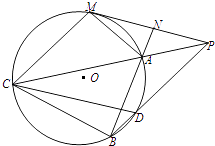
(1)求證:△APM∽△ABP;
(2)求證:四邊形PMCD是平行四邊形.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓M的方程為![]() ,直線l的方程為
,直線l的方程為![]() ,點P在直線l上,過點P作圓M的切線PA,PB,切點為A,B.
,點P在直線l上,過點P作圓M的切線PA,PB,切點為A,B.
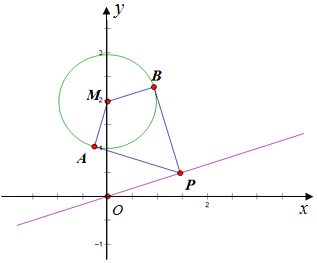
![]() 若
若![]() ,試求點P的坐標;
,試求點P的坐標;
![]() 求四邊形PAMB面積的最小值及此時點P的坐標;
求四邊形PAMB面積的最小值及此時點P的坐標;
![]() 求證:經過A,P,M三點的圓必過定點,并求出所有定點的坐標.
求證:經過A,P,M三點的圓必過定點,并求出所有定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2ax-![]() x2-3ln x,其中a∈R,為常數.
x2-3ln x,其中a∈R,為常數.
(1)若f(x)在x∈[1,+∞)上是減函數,求實數a的取值范圍;
(2)若x=3是f(x)的極值點,求f(x)在x∈[1,a]上的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】盒子里裝有大小質量完全相同且分別標有數字1、2、3、4的四個小球,從盒子里隨機摸出兩個小球,那么事件“摸出的小球上標有的數字之和大于數字之積”的概率是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列四個命題,其中正確命題的個數( )
①若a>|b|,則a2>b2
②若a>b,c>d,則a﹣c>b﹣d
③若a>b,c>d,則ac>bd
④若a>b>o,則 ![]() >
> ![]() .
.
A.3個
B.2個
C.1個
D.0個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() ,
,![]() ,
,![]() 在拋物線
在拋物線![]() 上,
上,![]() 的重心與此拋物線的焦點
的重心與此拋物線的焦點![]() 重合(如圖)
重合(如圖)

(I)寫出該拋物線的方程和焦點![]() 的坐標;
的坐標;
(II)求線段![]() 中點
中點![]() 的坐標;
的坐標;
(III)求弦![]() 所在直線的方程
所在直線的方程
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com