【題目】設
，函數
．
（1）當
時，求
在
上的單調區(qū)間；
（2）設函數
，當
有兩個極值點
時，總有
，求實數
的值．
【答案】（1）增區(qū)間是
，減區(qū)間是
；（2）
.
【解析】試題分析：
(1)利用導函數與原函數的關系結合函數的解析式可得函數的增區(qū)間是
，減區(qū)間是
；
(2)利用題意結合導函數的性質可得
.
試題解析：
（1）當
時，
，
則
，令
，則
.
易知
在
上單調遞減，又
所以
在上單調遞減，又因為
，
所以當
時，
，從而
，這時
單調遞增，
當
時，
，從而
，這時單調遞減.
所以在上的增區(qū)間是 
減區(qū)間是
（2）由題可知
，則
.
根據題意方程
有兩個不等實數根
且
，
令
得
，且
，所以
由
，其中
，
得
.將
代入左式得：
，整理得
.
即不等式對任意
恒成立.
①當
時，得
②當
時，即
令
，易知
是
上的減函數，
所以
，所以
③當
時，即
.
在
上也是減函數，
,所以
綜上所述
智慧小復習系列答案科目：高中數學 來源： 題型：
【題目】設函數f(x)＝ln x－ax(a∈R)(e＝2.718 28…是自然對數的底數)．
(1)判斷f(x)的單調性；
(2)當f(x)<0在(0，＋∞)上恒成立時，求a的取值范圍；
(3)證明：當x∈(0，＋∞)時，
(1＋x) 
<e.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校學生研究性學習小組發(fā)現，學生上課的注意力指標隨著聽課時間的變化而變化，老師講課開始時，學生的興趣激增；接下來學生的興趣將保持較理想的狀態(tài)一段時間，隨后學生的注意力開始分散．設 
表示學生注意力指標，該小組發(fā)現 
隨時間 
（分鐘）的變化規(guī)律（
越大，表明學生的注意力越集中）如下： 
（
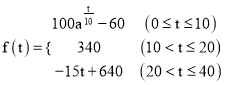，且 
）
若上課后第 
分鐘時的注意力指標為 
，回答下列問題：
（1）求 
的值；
（2）上課后第 
分鐘時和下課前 
分鐘時比較，哪個時間注意力更集中?并請說明理由．
（3）在一節(jié)課中，學生的注意力指標至少達到 
的時間能保持多長?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示是某企業(yè)2010年至2016年污水凈化量（單位: 噸）的折線圖.
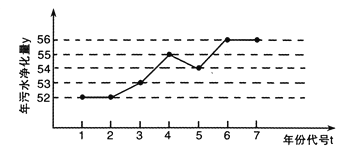
注: 年份代碼1-7分別對應年份2010-2016.
（1）由折線圖看出，可用線性回歸模型擬合
和
的關系，請用相關系數加以說明；
（2）建立關于的回歸方程，預測
年該企業(yè)污水凈化量；
（3）請用數據說明回歸方程預報的效果.
附注: 參考數據:
；
參考公式：相關系數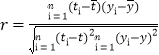
，回歸方程
中斜率和截距的最小；
二乘法估汁公式分別為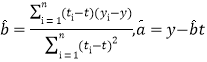
；
反映回歸效果的公式為：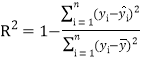
，其中
越接近于
，表示回歸的效果越好.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了研究家用轎車在高速公路上的車速情況，交通部門對100名家用轎車駕駛員進行調查，得到其在高速公路上行駛時的平均車速情況為：在55名男性駕駛員中，平均車速超過100km/h的有40人，不超過100km/h的有15人．在45名女性駕駛員中，平均車速超過100km/h的有20人，不超過100km/h的有25人．
（1）完成下面的列聯(lián)表，并判斷是否有99.5%的把握認為平均車速超過100km/h的人與性別有關．
平均車速超過 100km/h人數 | 平均車速不超過 100km/h人數 | 合計 | |
男性駕駛員人數 | |||
女性駕駛員人數 | |||
合計 |
（2）以上述數據樣本來估計總體，現從高速公路上行駛的大量家用轎車中隨機抽取3輛，記這3輛車中駕駛員為男性且車速超過100km/h的車輛數為
，若每次抽取的結果是相互獨立的，求
的分布列和數學期望．
參考公式與數據：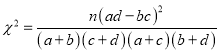 
，其中
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
