
【題目】函數(shù)![]() (其中
(其中![]() )的部分圖象如圖所示,把函數(shù)
)的部分圖象如圖所示,把函數(shù)![]() 的圖像向右平移
的圖像向右平移![]() 個單位長度,再向下平移
個單位長度,再向下平移![]() 個單位,得到函數(shù)
個單位,得到函數(shù)![]() 的圖像。
的圖像。

(1)當(dāng)![]() 時,若方程
時,若方程![]() 恰好有兩個不同的根
恰好有兩個不同的根![]() ,求
,求![]() 的取值范圍及
的取值范圍及![]() 的值;
的值;
(2)令![]() ,若對任意
,若對任意![]() 都有
都有![]() 恒成立,求
恒成立,求![]() 的最大值
的最大值
【答案】(1)![]() 時,
時,![]() ;
;![]() 時,
時,![]()
(2)![]()
【解析】
(1)根據(jù)給出的圖像求出![]() 解析式,再根據(jù)平移得到
解析式,再根據(jù)平移得到![]() 解析式由
解析式由![]() 的范圍求出
的范圍求出![]() 的單調(diào)區(qū)間和值域,結(jié)合圖像,分析出
的單調(diào)區(qū)間和值域,結(jié)合圖像,分析出![]() 的范圍及
的范圍及![]() 的值.
的值.
(2)令![]()
![]() ,得到
,得到![]() ,是關(guān)于
,是關(guān)于![]() 的二次函數(shù),利用二次函數(shù)的保號性,得到答案.
的二次函數(shù),利用二次函數(shù)的保號性,得到答案.
(1)根據(jù)圖像可知![]()
![]() ,
,![]()
代入![]() 得,
得,![]() ,
,![]() ,
,
![]()
![]()
把函數(shù)![]() 的圖像向右平移
的圖像向右平移![]() 個單位長度,再向下平移
個單位長度,再向下平移![]() 個單位,得到函數(shù)
個單位,得到函數(shù)
![]()
![]() 在
在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減,在
單調(diào)遞減,在![]() 單調(diào)遞增,
單調(diào)遞增,
且![]() ,
,![]()
![]() ,
,![]()
方程![]() 恰好有兩個不同的根
恰好有兩個不同的根![]() ,
,
![]() 的取值范圍
的取值范圍![]()
令![]()
![]()
![]() 對稱軸為
對稱軸為![]() ,
,![]()
![]()
![]() 或
或![]()
![]()
![]() 時,
時,![]() ;
;![]() 時,
時,![]() .
.
(2)由(1)可知![]()
![]()
![]()
對任意![]() 都有
都有![]() 恒成立
恒成立
令![]()
![]() ,是關(guān)于
,是關(guān)于![]() 的二次函數(shù),開口向上
的二次函數(shù),開口向上
則![]() 恒成立
恒成立
而![]() 的最大值,在
的最大值,在![]() 或
或![]() 時取到最大值
時取到最大值
則![]() ,
,![]() 解得
解得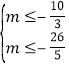
所以![]() ,則
,則![]() 的最大值為
的最大值為![]() .
.


 亮點(diǎn)激活精編提優(yōu)100分大試卷系列答案
亮點(diǎn)激活精編提優(yōu)100分大試卷系列答案 智趣寒假作業(yè)云南科技出版社系列答案
智趣寒假作業(yè)云南科技出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分) 某中學(xué)的環(huán)保社團(tuán)參照國家環(huán)境標(biāo)準(zhǔn)制定了該校所在區(qū)域空氣質(zhì)量指數(shù)與空氣質(zhì)量等級對應(yīng)關(guān)系如下表(假設(shè)該區(qū)域空氣質(zhì)量指數(shù)不會超過![]() ):
):
空氣質(zhì)量指數(shù) |
|
|
|
|
|
|
空氣質(zhì)量等級 |
|
|
|
|
|
|
該社團(tuán)將該校區(qū)在![]() 年
年![]() 天的空氣質(zhì)量指數(shù)監(jiān)測數(shù)據(jù)作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.
天的空氣質(zhì)量指數(shù)監(jiān)測數(shù)據(jù)作為樣本,繪制的頻率分布直方圖如下圖,把該直方圖所得頻率估計為概率.
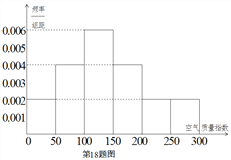
(Ⅰ)請估算![]() 年(以
年(以![]() 天計算)全年空氣質(zhì)量優(yōu)良的天數(shù)(未滿一天按一天計算);
天計算)全年空氣質(zhì)量優(yōu)良的天數(shù)(未滿一天按一天計算);
(Ⅱ)該校![]() 年
年![]() 月
月![]() 、
、![]() 日將作為高考考場,若這兩天中某天出現(xiàn)
日將作為高考考場,若這兩天中某天出現(xiàn)![]() 級重度污染,需要凈化空氣費(fèi)用
級重度污染,需要凈化空氣費(fèi)用![]() 元,出現(xiàn)
元,出現(xiàn)![]() 級嚴(yán)重污染,需要凈化空氣費(fèi)用
級嚴(yán)重污染,需要凈化空氣費(fèi)用![]() 元,記這兩天凈化空氣總費(fèi)用為
元,記這兩天凈化空氣總費(fèi)用為![]() 元,求
元,求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x),g(x)的定義域都是D,直線x=x0(x0∈D),與y=f(x),y=g(x)的圖象分別交于A,B兩點(diǎn),若|AB|的值是不等于0的常數(shù),則稱曲線 y=f(x),y=g(x)為“平行曲線”,設(shè)f(x)=ex﹣alnx+c(a>0,c≠0),且y=f(x),y=g(x)為區(qū)間(0,+∞)的“平行曲線”,g(1)=e,g(x)在區(qū)間(2,3)上的零點(diǎn)唯一,則a的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() ,在
,在![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() ,
, ![]() ;
;
(2)若![]() ,證明:
,證明: ![]() .
.
【答案】(1)![]() ,
, ![]() ;(2)見解析
;(2)見解析
【解析】試題分析:(1)求出函數(shù)的導(dǎo)數(shù),得到關(guān)于![]() 的方程組,解出即可;
的方程組,解出即可;
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,令
,令![]() , 利用導(dǎo)數(shù)研究其單調(diào)性可得
, 利用導(dǎo)數(shù)研究其單調(diào)性可得
![]() ,
,
從而證明![]() .
.
試題解析:((1)由題意![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
若![]() ,則
,則![]() ,與
,與![]() 矛盾,故
矛盾,故![]() ,
, ![]() .
.
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,
,
令![]() ,
,
![]() ,
,
令![]()
當(dāng)![]() 時,
時, ![]() ,
, ![]() 單調(diào)遞減,且
單調(diào)遞減,且![]() ;
;
當(dāng)![]() 時,
時, ![]() ,
, ![]() 單調(diào)遞增;且
單調(diào)遞增;且![]() ,
,
所以![]() 在
在![]() 上當(dāng)單調(diào)遞減,在
上當(dāng)單調(diào)遞減,在![]() 上單調(diào)遞增,且
上單調(diào)遞增,且![]() ,
,
故![]() ,
,
故![]() .
.
【點(diǎn)睛】本題考查利用函數(shù)的切線求參數(shù)的方法,以及利用導(dǎo)數(shù)證明不等式的方法,解題時要認(rèn)真審題,注意導(dǎo)數(shù)性質(zhì)的合理運(yùn)用.
【題型】解答題
【結(jié)束】
22
【題目】在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() ,
, ![]() 為參數(shù)),以坐標(biāo)原點(diǎn)
為參數(shù)),以坐標(biāo)原點(diǎn)![]() 為極點(diǎn),
為極點(diǎn), ![]() 軸正半軸為極軸建立極坐標(biāo)系,直線
軸正半軸為極軸建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 相切;
相切;
(1)求曲線![]() 的極坐標(biāo)方程;
的極坐標(biāo)方程;
(2)在曲線![]() 上取兩點(diǎn)
上取兩點(diǎn)![]() ,
, ![]() 與原點(diǎn)
與原點(diǎn)![]() 構(gòu)成
構(gòu)成![]() ,且滿足
,且滿足![]() ,求面積
,求面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知在數(shù)列{an}中, ![]() .,n∈N*
.,n∈N*
(1)求證:1<an+1<an<2;
(2)求證: ![]() ;
;
(3)求證:n<sn<n+2.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】柴靜《穹頂之下》的播出,讓大家對霧霾天氣的危害有了更進(jìn)一步的認(rèn)識,對于霧霾天氣的研究也漸漸活躍起來,某研究機(jī)構(gòu)對春節(jié)燃放煙花爆竹的天數(shù)x與霧霾天數(shù)y進(jìn)行統(tǒng)計分析,得出下表數(shù)據(jù):
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)請畫出上表數(shù)據(jù)的散點(diǎn)圖;
(2)請根據(jù)上表提供的數(shù)據(jù),用最小二乘法求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)試根據(jù)(2)求出的線性回歸方程,預(yù)測燃放煙花爆竹的天數(shù)為![]() 的霧霾天數(shù).
的霧霾天數(shù).

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com