
【題目】隨著互聯(lián)網(wǎng)的發(fā)展,移動支付![]() 又稱手機(jī)支付
又稱手機(jī)支付![]() 逐漸深入人民群眾的生活
逐漸深入人民群眾的生活![]() 某學(xué)校興趣小組為了了解移動支付在人民群眾中的熟知度,對
某學(xué)校興趣小組為了了解移動支付在人民群眾中的熟知度,對![]() 歲的人群隨機(jī)抽樣調(diào)查,調(diào)查的問題是你會使用移動支付嗎?”其中,回答“會”的共有50個人,把這50個人按照年齡分成5組,并繪制出頻率分布表
歲的人群隨機(jī)抽樣調(diào)查,調(diào)查的問題是你會使用移動支付嗎?”其中,回答“會”的共有50個人,把這50個人按照年齡分成5組,并繪制出頻率分布表![]() 部分?jǐn)?shù)據(jù)模糊不清
部分?jǐn)?shù)據(jù)模糊不清![]() 如表:
如表:
分組 | 頻數(shù) | 頻率 | |
第1組 |
| 10 |
|
第2組 |
|
|
|
第3組 |
| 15 |
|
第4組 |
|
|
|
第5組 |
| 2 |
|
合計 | 50 |
| |
![]() 表中
表中![]() 處的數(shù)據(jù)分別是多少?
處的數(shù)據(jù)分別是多少?
![]() 從第1組,第3組,第4組中用分層抽樣的方法抽取6人,求每組抽取的人數(shù).
從第1組,第3組,第4組中用分層抽樣的方法抽取6人,求每組抽取的人數(shù).
![]() 在
在![]() 抽取的6人中再隨機(jī)抽取2人,求所抽取的2人來自同一個組的概率.
抽取的6人中再隨機(jī)抽取2人,求所抽取的2人來自同一個組的概率.
【答案】(1)見解析;(2)見解析;(3)![]()
【解析】
![]() 由頻率分布表能求出表中
由頻率分布表能求出表中![]() 處的數(shù)據(jù).
處的數(shù)據(jù).![]() 從第1組,第3組,第4組中用分層抽樣的方法抽取6人,由第1組,第3組,第4組的人數(shù)之比為10:15:
從第1組,第3組,第4組中用分層抽樣的方法抽取6人,由第1組,第3組,第4組的人數(shù)之比為10:15:![]() :3:1,能求出結(jié)果.
:3:1,能求出結(jié)果.![]() 設(shè)從第1組抽取的2人為
設(shè)從第1組抽取的2人為![]() ,
,![]() ,從第3組抽取的3人為
,從第3組抽取的3人為![]() ,
,![]() ,
,![]() ,從第4組抽取的1人為C,從這6人中隨機(jī)抽取2人,利用列舉法能求出所抽取的2人來自同一個組的概率.
,從第4組抽取的1人為C,從這6人中隨機(jī)抽取2人,利用列舉法能求出所抽取的2人來自同一個組的概率.
![]() 由頻率分布表得:
由頻率分布表得:
![]() 處的數(shù)據(jù)是1,
處的數(shù)據(jù)是1,![]() 處的數(shù)據(jù)是:
處的數(shù)據(jù)是:![]() ,
,
![]() 處的數(shù)據(jù)是:
處的數(shù)據(jù)是:![]() ,
,
![]() 處的數(shù)據(jù)是:
處的數(shù)據(jù)是:![]() ,
,
![]() 處的數(shù)據(jù)是:
處的數(shù)據(jù)是:![]() .
.
![]() 第1組,第3組,第4組的人數(shù)之比為:
第1組,第3組,第4組的人數(shù)之比為:
10:15:![]() :3:1,
:3:1,
![]() 從第1組抽取的人數(shù)為:
從第1組抽取的人數(shù)為:![]() 人,
人,
從第3組抽取的人數(shù)為:![]() 人,
人,
從第4組抽取的人數(shù)為:![]() 人.
人.
![]() 設(shè)從第1組抽取的2人為
設(shè)從第1組抽取的2人為![]() ,
,![]() ,從第3組抽取的3人為
,從第3組抽取的3人為![]() ,
,![]() ,
,![]() ,從第4組抽取的1人為C,
,從第4組抽取的1人為C,
則從這6人中隨機(jī)抽取2人,基本事件有15個,分別為:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所抽取的2人來自同一個組包含的基本事件有4個,分別為:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 所抽取的2人來自同一個組的概率
所抽取的2人來自同一個組的概率![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知袋子中放有大小和形狀相同的小球若干,其中標(biāo)號為0的小球1個,標(biāo)號為1的小球1個,標(biāo)號為2的小球![]() 個.若從袋子中隨機(jī)抽取1個小球,取到標(biāo)號為2的小球的概率是
個.若從袋子中隨機(jī)抽取1個小球,取到標(biāo)號為2的小球的概率是![]() .
.
(1)求![]() 的值;
的值;
(2)從袋子中有放回地隨機(jī)抽取2個小球,記第一次取出的小球標(biāo)號為![]() ,第二次取出的小球標(biāo)號為
,第二次取出的小球標(biāo)號為![]() .
.
①記“![]() ”為事件
”為事件![]() ,求事件
,求事件![]() 的概率;
的概率;
②在區(qū)間![]() 內(nèi)任取2個實(shí)數(shù)
內(nèi)任取2個實(shí)數(shù)![]() ,求事件“
,求事件“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)的圖象在[a,b]上連續(xù)不斷,定義:
f1(x)=min{f(t)| a≤t≤x}(x∈[a,b]),
f2(x)=max{f(t)| a≤t≤x}(x∈[a,b])。
其中,min{f(x)| x∈D}表示函數(shù)f(x)在D上的最小值,max{f(x)|x∈D}表示函數(shù)f(x)在D上的最大值。若存在最小正整數(shù)k,使得f2(x)-f1(x)≤k(x-a)對任意的x∈[a,b]成立,則稱函數(shù)f(x)為[a,b]上的“k階收縮函數(shù)”。
(1)若f(x)=sinx,x∈[![]() ,
, ![]() ],請直接寫出f1(x),f2(x)的表達(dá)式;
],請直接寫出f1(x),f2(x)的表達(dá)式;
(2)已知函數(shù)f(x)=(x-1)2,x∈[-1,4],試判斷f(x)是否為[-1,4]上的“k階收縮函數(shù)”,如果是,求出對應(yīng)的k;如果不是,請說明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某興趣小組欲研究晝夜溫差大小與患感冒人數(shù)多少之間的關(guān)系,他們分別到氣象局與某醫(yī)院抄錄了 1至6月份每月10號的晝夜溫差情況與因患感冒而就診的人數(shù),得到如下資料:
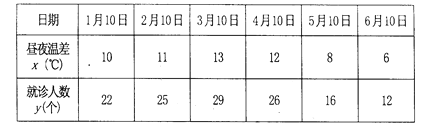
該興趣小組確定的研究方案是:先用2、3、4、5月的4組數(shù)據(jù)求線性回歸方程,再用1月和6月的2組數(shù)據(jù)進(jìn)行檢驗(yàn).
(1)請根據(jù)2、3、4、5月的數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若由線性回歸方程得到的估計數(shù)據(jù)與所選出的檢驗(yàn)數(shù)據(jù)的誤差均不超過2人,則認(rèn)為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?
(參考公式: 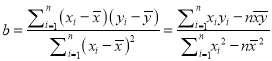 ,
, ![]() )
)
參考數(shù)據(jù): ![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某高級中學(xué)在今年“五一”期間給校內(nèi)所有教室安裝了同一型號的空調(diào),關(guān)于這批空調(diào)的使用年限![]() 單位:年
單位:年![]() 和所支出的維護(hù)費(fèi)用
和所支出的維護(hù)費(fèi)用![]() 單位:千元
單位:千元![]() 廠家提供的統(tǒng)計資料如表:
廠家提供的統(tǒng)計資料如表:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
![]() 若x與y之間是線性相關(guān)關(guān)系,請求出維護(hù)費(fèi)用y關(guān)于x的線性回歸直線方程
若x與y之間是線性相關(guān)關(guān)系,請求出維護(hù)費(fèi)用y關(guān)于x的線性回歸直線方程![]() ;
;
![]() 若規(guī)定當(dāng)維護(hù)費(fèi)用y超過
若規(guī)定當(dāng)維護(hù)費(fèi)用y超過![]() 千元時,該批空調(diào)必須報度,試根據(jù)
千元時,該批空調(diào)必須報度,試根據(jù)![]() 的結(jié)論求該批空調(diào)使用年限的最大值
的結(jié)論求該批空調(diào)使用年限的最大值![]() 結(jié)果取整數(shù)
結(jié)果取整數(shù)![]() 參考公式:
參考公式:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() 圖象上有且僅有四個不同的點(diǎn)關(guān)于直線y=e的對稱點(diǎn)在函數(shù)g(x)=kx+2e+1的圖象上,則實(shí)數(shù)k的取值范圍為( )
圖象上有且僅有四個不同的點(diǎn)關(guān)于直線y=e的對稱點(diǎn)在函數(shù)g(x)=kx+2e+1的圖象上,則實(shí)數(shù)k的取值范圍為( )
A.(1,2)
B.(﹣1,0)
C.(﹣2,﹣1)
D.(﹣6,﹣1)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系內(nèi),已知點(diǎn)![]() ,
,![]() ,圓C的方程為
,圓C的方程為![]() ,點(diǎn)P為圓上的動點(diǎn).
,點(diǎn)P為圓上的動點(diǎn).
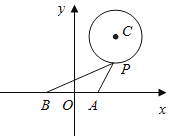
![]() 求過點(diǎn)A的圓C的切線方程.
求過點(diǎn)A的圓C的切線方程.
![]() 求
求![]() 的最大值及此時對應(yīng)的點(diǎn)P的坐標(biāo).
的最大值及此時對應(yīng)的點(diǎn)P的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義在非零實(shí)數(shù)集上的函數(shù)![]() 滿足
滿足![]() ,且
,且![]() 是區(qū)間
是區(qū)間![]() 上的遞增函數(shù).
上的遞增函數(shù).
(1)求![]() 的值;
的值;
(2)求證: ![]() ;
;
(3)解不等式![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的菱形,
的菱形, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上的一個點(diǎn),
上的一個點(diǎn), ![]() ,
, ![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).
(1)證明: ![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com