
【題目】已知三棱柱![]() 中,
中, ![]() ,側(cè)面
,側(cè)面![]() 底面
底面![]() ,
, ![]() 是
是![]() 的中點,
的中點, ![]() .
.
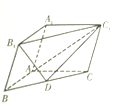
(Ⅰ)求證: ![]() 面
面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成線面角的正弦值.
所成線面角的正弦值.
【答案】(Ⅰ)證明見解析;(Ⅱ) ![]() .
.
【解析】試題分析:
(Ⅰ)由題意可證得側(cè)面![]() 底面
底面![]() 于
于![]() ,而
,而![]() 在底面
在底面![]() 內(nèi),故
內(nèi),故![]() 面
面![]() .
.
(Ⅱ)首先做出直線與平面所成的角,然后結(jié)合結(jié)合關(guān)系整理計算即可求得直線![]() 與平面
與平面![]() 所成線面角的正弦值是
所成線面角的正弦值是![]() .
.
試題解析:
(Ⅰ)取![]() 中點
中點![]() ,連接
,連接![]() ,
,
![]() 中,
中, ![]() ,故
,故![]() 是等邊三角形,∴
是等邊三角形,∴![]() ,
,
又![]() ,而
,而![]() 與
與![]() 相交于
相交于![]() ,∴
,∴![]() 面
面![]() ,
,
故![]() ,又
,又![]() ,所以
,所以![]() ,
,
又∵側(cè)面![]() 底面
底面![]() 于
于![]() ,
, ![]() 在底面
在底面![]() 內(nèi),∴
內(nèi),∴![]() 面
面![]() .
.
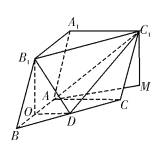
(Ⅱ)過![]() 作
作![]() 平面
平面![]() ,垂足為
,垂足為![]() ,連接
,連接![]() ,
, ![]() 即為直線
即為直線![]() 與平面
與平面![]() 所成的角,
所成的角,
由(Ⅰ)知![]() ,側(cè)面
,側(cè)面![]() 底面
底面![]() ,所以
,所以![]() 平面
平面![]() ,由等邊
,由等邊![]() 知
知![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() ,
,
由(Ⅰ)知![]() 面
面![]() ,所以
,所以![]() ,∴四邊形
,∴四邊形![]() 是正方形,
是正方形,
∵![]() ,∴
,∴![]() ,
,
∴在![]() 中,
中, ![]() ,
,
所以直線![]() 與平面
與平面![]() 所成線面角的正弦值為
所成線面角的正弦值為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,
, ![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)令![]() ,設(shè)數(shù)列
,設(shè)數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,求
,求![]() ;
;
(3)令![]() ,若
,若![]() 對
對![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】我國古代數(shù)學(xué)著作《九章算術(shù)》有如下問題:“今有蒲(水生植物名)生一日,長三尺;莞(植物名,俗稱水蔥、席子草)生一日,長一尺.蒲生日自半,莞生日自倍.問幾何日而長等?”意思是:今有蒲生長1日,長為3尺;莞生長1日,長為1尺.蒲的生長逐日減半,莞的生長逐日增加1倍.若蒲、莞長度相等,則所需的時間約為(結(jié)果保留一位小數(shù).參考數(shù)據(jù):![]() ,
,![]() )
)
A.1.3日 B.1.5日
C.2.6日 D.2.8日
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=3x+λ3﹣x(λ∈R).
(1)當λ=﹣4時,求函數(shù)f(x)的零點;
(2)若函數(shù)f(x)為偶函數(shù),求實數(shù)λ的值;
(3)若不等式f(x)≤6在x∈[0,2]上恒成立,求實數(shù)λ的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在平面直角坐標系![]() 中,以
中,以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系.若直線
軸的正半軸為極軸建立極坐標系.若直線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,將曲線
,將曲線![]() 上所有點的橫坐標縮短為原來的一半,縱坐標不變,然后再向右平移一個單位得到曲線
上所有點的橫坐標縮短為原來的一半,縱坐標不變,然后再向右平移一個單位得到曲線![]() .
.
(Ⅰ)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,點
兩點,點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知平行四邊形![]() 的三個頂點的坐標為
的三個頂點的坐標為![]() ,
, ![]() ,
, ![]() .
.
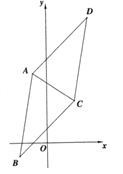
(1)求平行四邊形![]() 的頂點
的頂點![]() 的坐標;
的坐標;
(2)在![]() 中,求
中,求![]() 邊上的高所在直線方程;
邊上的高所在直線方程;
(3)求四邊形![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)是定義域為R上的奇函數(shù),當x>0時,f(x)=x2+2x.
(1)求f(x)的解析式;
(2)若不等式f(t﹣2)+f(2t+1)>0成立,求實數(shù)t的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=log4(4x+1)+kx(k∈R)是偶函數(shù).
(1)求實數(shù)k的值;
(2)設(shè)g(x)=log4(a2x+a),若f(x)=g(x)有且只有一個實數(shù)解,求實數(shù)a的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com