Question

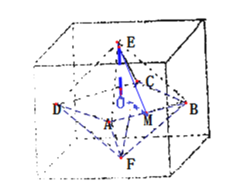
【題目】連接正方體每個面的中心構成一個正八面體，則該八面體的外接球與內切球體積之比為______．

Answer 1

【答案】.

【解析】

正八面體中ABCD四點或AFCE四點所組成的截面在外接球的一個大圓面上，可得其對角線的長度即為外接球的直徑，又正方體中心設為O，取AB中點M，則在直角△OME中，斜邊ME上的高即為內切球的半徑，由此能求出結果．

若正八面體的外接球的各個頂點都在同一個球面上，

則其中ABCD四點或AFCE四點所組成的截面在球的一個大圓面上，

可得，此四點組成的正方形是球的大圓的一個內接正方形，

其對角線的長度即為球的直徑，

設正八面體邊長為2，且每個側面三角形均為等邊三角形，

故FE=AC=2，則外接球的半徑是，

又正方體中心設為O，取AB中點M，則在直角△OME中，斜邊ME==，

斜邊ME上的高即為內切球的半徑，大小為=，

∴外接球與內切球半徑之比為，∴外接球與內切球體積之比為

故答案為．