
(本題滿分18分) 本題共有3個小題,第1小題滿分4分,第2小題滿分6分. 第3小題滿分8分.
(理)對于數(shù)列 ,從中選取若干項,不改變它們在原來數(shù)列中的先后次序,得到的數(shù)列稱為是原來數(shù)列的一個子數(shù)列. 某同學(xué)在學(xué)習(xí)了這一個概念之后,打算研究首項為正整數(shù)
,從中選取若干項,不改變它們在原來數(shù)列中的先后次序,得到的數(shù)列稱為是原來數(shù)列的一個子數(shù)列. 某同學(xué)在學(xué)習(xí)了這一個概念之后,打算研究首項為正整數(shù) ,公比為正整數(shù)
,公比為正整數(shù)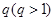 的無窮等比數(shù)列
的無窮等比數(shù)列 的子數(shù)列問題. 為此,他任取了其中三項
的子數(shù)列問題. 為此,他任取了其中三項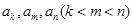 .
.
(1) 若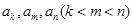 成等比數(shù)列,求
成等比數(shù)列,求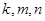 之間滿足的等量關(guān)系;
之間滿足的等量關(guān)系;
(2) 他猜想:“在上述數(shù)列 中存在一個子數(shù)列
中存在一個子數(shù)列 是等差數(shù)列”,為此,他研究了
是等差數(shù)列”,為此,他研究了 與
與 的大小關(guān)系,請你根據(jù)該同學(xué)的研究結(jié)果來判斷上述猜想是否正確;
的大小關(guān)系,請你根據(jù)該同學(xué)的研究結(jié)果來判斷上述猜想是否正確;
(3) 他又想:在首項為正整數(shù) ,公差為正整數(shù)
,公差為正整數(shù) 的無窮等差數(shù)列中是否存在成等比數(shù)列的子數(shù)列?請你就此問題寫出一個正確命題,并加以證明.
的無窮等差數(shù)列中是否存在成等比數(shù)列的子數(shù)列?請你就此問題寫出一個正確命題,并加以證明.
(1)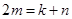 ;(2)不成立;(3) 對于首項為正整數(shù)
;(2)不成立;(3) 對于首項為正整數(shù) ,公差為正整數(shù)
,公差為正整數(shù) 的無窮等差數(shù)列
的無窮等差數(shù)列 ,總可以找到一個無窮子數(shù)列
,總可以找到一個無窮子數(shù)列 ,使得
,使得 是一個等比數(shù)列.
是一個等比數(shù)列.
解析試題分析:(1)由已知可得: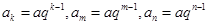 , 1分
, 1分
則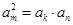 ,即有
,即有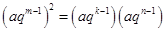 , 3分
, 3分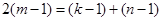 ,化簡可得.
,化簡可得. 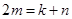 . 4分
. 4分
(2) 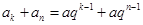 ,又
,又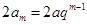 ,
,
故  , 6分
, 6分
由于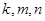 是正整數(shù),且
是正整數(shù),且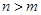 ,則
,則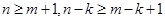 ,
,
又 是滿足
是滿足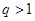 的正整數(shù),則
的正整數(shù),則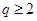 ,
, ,
,
所以, >
> ,從而上述猜想不成立. 10分
,從而上述猜想不成立. 10分
(3)命題:對于首項為正整數(shù) ,公差為正整數(shù)
,公差為正整數(shù) 的無窮等差數(shù)列
的無窮等差數(shù)列 ,總可以找到一個無窮子數(shù)列
,總可以找到一個無窮子數(shù)列 ,使得
,使得 是一個等比數(shù)列. 13分
是一個等比數(shù)列. 13分
此命題是真命題,下面我們給出證明.
證法一: 只要證明對任意正整數(shù)n,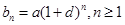 都在數(shù)列{an}中.因為bn=a(1+d)n=a(1+
都在數(shù)列{an}中.因為bn=a(1+d)n=a(1+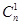 d+
d+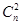 d2+…+
d2+…+ dn)=a(Md+1),這里M=
dn)=a(Md+1),這里M=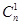 +
+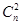 d+…+
d+…+ dn-1為正整數(shù),所以a(Md+1)=a+aMd是{an}中的第aM+1項,證畢. 18分
dn-1為正整數(shù),所以a(Md+1)=a+aMd是{an}中的第aM+1項,證畢. 18分
證法二:首項為 ,公差為
,公差為 (
( 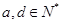 )的等差數(shù)列為
)的等差數(shù)列為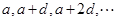 ,考慮數(shù)列
,考慮數(shù)列 中的項:
中的項: 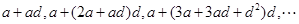
依次取數(shù)列 中項
中項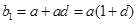 ,
,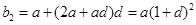 ,
,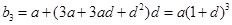 ,則由
,則由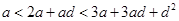 ,可知
,可知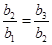 ,并由數(shù)學(xué)歸納法可知,數(shù)列
,并由數(shù)學(xué)歸納法可知,數(shù)列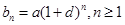 為
為 的無窮等比子數(shù)列. 18分
的無窮等比子數(shù)列. 18分
考點:等比數(shù)列的簡單性質(zhì);數(shù)列的綜合應(yīng)用。
點評:此題考查了等差數(shù)列的性質(zhì)即通項公式,同時本題屬于新定義及結(jié)論探索性問題,這類試題的一般解法是:充分抓住已知條件,找準(zhǔn)問題的突破點,由淺入深,多角度、多側(cè)面探尋,聯(lián)系符合題設(shè)的有關(guān)知識,合理組合發(fā)現(xiàn)新結(jié)論,圍繞所探究的結(jié)論環(huán)環(huán)相扣,步步逼近發(fā)現(xiàn)規(guī)律,得出結(jié)論.熟練掌握公式及性質(zhì)是解本題的關(guān)鍵.


科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)正項數(shù)列 都是等差數(shù)列,且公差相等,(1)求
都是等差數(shù)列,且公差相等,(1)求 的通項公式;(2)若
的通項公式;(2)若 的前三項,記數(shù)列
的前三項,記數(shù)列 數(shù)列
數(shù)列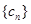 的前n項和為
的前n項和為
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分16分)
已知有窮數(shù)列 共有
共有 項(整數(shù)
項(整數(shù) ),首項
),首項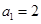 ,設(shè)該數(shù)列的前
,設(shè)該數(shù)列的前 項和為
項和為 ,且
,且 其中常數(shù)
其中常數(shù) ⑴求
⑴求 的通項公式;⑵若
的通項公式;⑵若 ,數(shù)列
,數(shù)列 滿足
滿足
求證: ;
;
⑶若⑵中數(shù)列 滿足不等式:
滿足不等式: ,求
,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知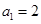 ,點
,點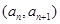 在函數(shù)
在函數(shù)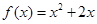 的圖象上,其中
的圖象上,其中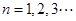
(1)證明數(shù)列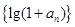 是等比數(shù)列;
是等比數(shù)列;
(2)設(shè)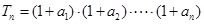 ,求
,求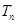 及數(shù)列
及數(shù)列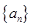 的通項;
的通項;
(3)記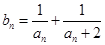 ,求數(shù)列
,求數(shù)列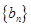 的前
的前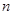 項和
項和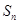 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分13分)設(shè)數(shù)列 為單調(diào)遞增的等差數(shù)列
為單調(diào)遞增的等差數(shù)列 且
且 依次成等比數(shù)列.
依次成等比數(shù)列.
(Ⅰ)求數(shù)列 的通項公式
的通項公式 ;
;
(Ⅱ)若 求數(shù)列
求數(shù)列 的前
的前 項和
項和 ;
;
(Ⅲ)若 ,求證:
,求證:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)數(shù)列 的前n項和為Sn=2n2,
的前n項和為Sn=2n2, 為等比數(shù)列,且
為等比數(shù)列,且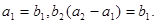
(Ⅰ)求數(shù)列 和
和 的通項公式;
的通項公式;
(Ⅱ)設(shè)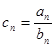 ,求數(shù)列
,求數(shù)列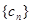 前n項和Tn.
前n項和Tn.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分) 已知曲線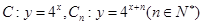 ,從
,從 上的點
上的點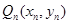 作
作 軸的垂線,交
軸的垂線,交 于點
于點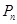 ,再從點
,再從點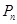 作
作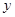 軸的垂線,交
軸的垂線,交 于點
于點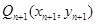 ,
,
設(shè)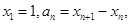
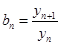 .。
.。 求數(shù)列
求數(shù)列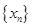 的通項公式;
的通項公式;  記
記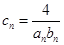 ,數(shù)列
,數(shù)列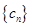 的前
的前 項和為
項和為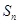 ,試比較
,試比較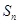 與
與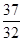 的大小
的大小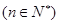 ;
;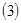 記
記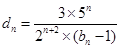 ,數(shù)列
,數(shù)列 的前
的前 項和為
項和為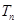 ,試證明:
,試證明: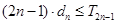 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分14分)
已知數(shù)列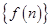 的前n項和為
的前n項和為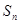 ,且
,且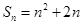 .
.
(Ⅰ)求數(shù)列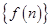 通項公式;
通項公式;
(Ⅱ)若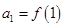 ,
,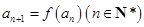 ,求證數(shù)列
,求證數(shù)列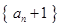 是等比數(shù)列,并求數(shù)
是等比數(shù)列,并求數(shù)
列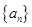 的前
的前 項和
項和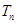 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
某工廠用7萬元錢購買了一臺新機器,運輸安裝費用2千元,每年投保、動力消耗的費用也為2千元,每年的保養(yǎng)、維修、更換易損零件的費用逐年增加,第一年為2千元,第二年為3千元,第三年為4千元,依此類推,即每年增加1千元.問這臺機器最佳使用年限是多少年?并求出年平均費用的最小值.(最佳使用年限佳是使年平均費用最小的時間)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com