Question

【題目】某廠擬用集裝箱托運甲、乙兩種貨物，集裝箱的體積、重量、可獲利潤和托運能力等限制數(shù)據(jù)列在表中，如何設(shè)計甲、乙兩種貨物應(yīng)各托運的箱數(shù)可以獲得最大利潤，最大利潤是多少？

貨物	體積箱	重量箱	利潤百元箱
甲	5	2	20
乙	4	5	10
托運限制	24	13

Answer 1

【答案】當托運甲4箱，乙1箱時利潤最大，最大利潤為9000元。

【解析】

試題首先設(shè)甲、乙兩種貨物應(yīng)各托運的箱數(shù)為x，y，由已知條件和表格中的數(shù)據(jù)得到的線性約束條件，將所求的利用用表示，將實際問題轉(zhuǎn)化為線性規(guī)劃求最值問題

試題解析：設(shè)甲、乙兩種貨物應(yīng)各托運的箱數(shù)為x，y，則

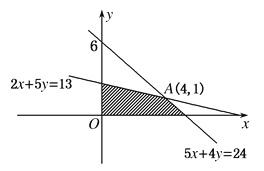
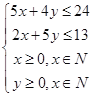
目標函數(shù)z＝20x＋10y，畫出可行域如圖．

由得A（4,1）．

易知當直線2x＋y＝0平移經(jīng)過點A（4,1）時，z取得最大值．且

答：當托運甲4箱，乙1箱時利潤最大，最大利潤為9000元。