
設函數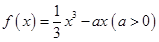 ,
,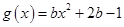 .
.
(1)若曲線 與
與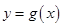 在它們的交點
在它們的交點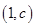 處有相同的切線,求實數
處有相同的切線,求實數 、
、 的值;
的值;
(2)當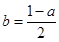 時,若函數
時,若函數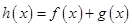 在區(qū)間
在區(qū)間 內恰有兩個零點,求實數
內恰有兩個零點,求實數 的取值范圍;
的取值范圍;
(3)當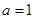 ,
,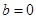 時,求函數
時,求函數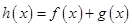 在區(qū)間
在區(qū)間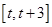 上的最小值.
上的最小值.
(1) ;(2)
;(2)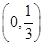 ;(3)
;(3) .
.
解析試題分析:(1)從條件“曲線 與
與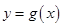 在它們的交點
在它們的交點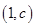 處有相同的切線”得到
處有相同的切線”得到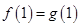 以及
以及 ,從而列有關
,從而列有關 、
、 的二元方程組,從而求出
的二元方程組,從而求出 與
與 的值;(2)將
的值;(2)將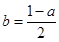 代入函數
代入函數 的解析式,利用導數分析函數
的解析式,利用導數分析函數 在區(qū)間
在區(qū)間 上的單調性,確定函數
上的單調性,確定函數 在區(qū)間
在區(qū)間 上是單峰函數后,然后對函數
上是單峰函數后,然后對函數 的端點值與峰值進行限制,列不等式組解出
的端點值與峰值進行限制,列不等式組解出 的取值范圍;(3)將
的取值范圍;(3)將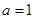 ,
,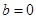 代入函數
代入函數 的解析式,并求出函數
的解析式,并求出函數 的單調區(qū)間,對函數
的單調區(qū)間,對函數 的極值點是否在區(qū)間
的極值點是否在區(qū)間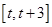 內進行分類討論,結合函數的單調性確定函數
內進行分類討論,結合函數的單調性確定函數 在區(qū)間
在區(qū)間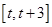 上的最小值.
上的最小值.
試題解析:(1)因為 ,
,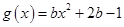 ,所以
,所以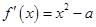 ,
,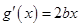 .
.
因為曲線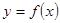 與
與 在它們的交點
在它們的交點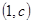 處有相同切線,
處有相同切線,
所以 ,且
,且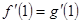 ,
,
即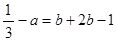 ,且
,且 ,解得
,解得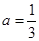 ,
, ;
;
(2)當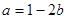 時,
時,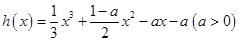 ,
,
所以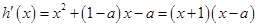 ,
,
令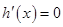 ,解得
,解得 ,
,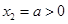 ,
,
當 變化時,
變化時, 、
、 的變化情況如下表:
的變化情況如下表: