
【題目】已知函數![]() (
(![]() ,
, ![]() 為常數),函數
為常數),函數![]() (
(![]() 為自然對數的底).
為自然對數的底).
(1)討論函數![]() 的極值點的個數;
的極值點的個數;
(2)若不等式![]() 對
對![]() 恒成立,求實數的
恒成立,求實數的![]() 取值范圍.
取值范圍.
【答案】(1)詳見解析(2)![]()
【解析】試題分析:(1)求得![]()
![]()
![]() ,分三種情況討論,分別研究函數的單調性進而可得函數極值點的個數;(2)不等式
,分三種情況討論,分別研究函數的單調性進而可得函數極值點的個數;(2)不等式![]() 對
對![]() 恒成立,等價于
恒成立,等價于![]() 只需研究函數
只需研究函數![]() 的最小值不小于零即可.
的最小值不小于零即可.
試題解析:(1)![]()
![]()
![]() ,
,
由![]() 得:
得: ![]() ,記
,記![]() ,則
,則![]() ,
,
由![]() 得
得![]() ,且
,且![]() 時,
時, ![]() ,
, ![]() 時,
時, ![]() ,
,
所以當![]() 時,
時, ![]() 取得最大值
取得最大值![]() ,又
,又![]() ,
,
(i)當![]() 時,
時, ![]() 恒成立,函數
恒成立,函數![]() 無極值點;
無極值點;
(ii)當![]() 時,
時, ![]() 有兩個解
有兩個解![]() ,
, ![]() ,且
,且![]() 時,
時, ![]() ,
, ![]() 時,
時, ![]() ,
, ![]() 時,
時, ![]() ,所以函數
,所以函數![]() 有兩個極值點;
有兩個極值點;
(iii)當![]() 時,方程
時,方程![]() 有一個解
有一個解![]() ,且
,且![]() 時
時![]() ,
, ![]() 時,
時, ![]() ,所以函數
,所以函數![]() 有一個極值點;
有一個極值點;
(2)記![]()
![]()
![]() ,
,
由![]() ,
,
![]() ,
, ![]() ,
,
由![]() ,
,
又當![]() ,
, ![]() 時,
時, ![]()
![]() ,
,
![]() ,
, ![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
所以![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
綜上實數![]() 的取值范圍是
的取值范圍是![]() .
.
【方法點晴】本題主要考查利用導數求函數的最值以及不等式恒成立問題,屬于難題.不等式恒成立問題常見方法:① 分離參數![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 數形結合(
即可);② 數形結合(![]() 圖象在
圖象在![]() 上方即可);③ 討論最值
上方即可);③ 討論最值![]() 或
或![]() 恒成立;④ 討論參數.本題是利用方法 ③ 求得
恒成立;④ 討論參數.本題是利用方法 ③ 求得![]() 的范圍的.
的范圍的.


科目:高中數學 來源: 題型:
【題目】已知{an}是公差為1的等差數列,a1 , a5 , a25成等比數列.
(1)求數列{an}的通項公式;
(2)設bn= ![]() 3+an , 求數列{bn}的前n項和Tn .
3+an , 求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】東莞市某高級中學在今年4月份安裝了一批空調,關于這批空調的使用年限![]() (單位:年,
(單位:年, ![]() )和所支出的維護費用
)和所支出的維護費用![]() (單位:萬元)廠家提供的統計資料如下:
(單位:萬元)廠家提供的統計資料如下:

(1)請根據以上數據,用最小二乘法原理求出維護費用![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若規定當維護費用![]() 超過13.1萬元時,該批空調必須報廢,試根據(1)的結論預測該批空調使用年限的最大值.
超過13.1萬元時,該批空調必須報廢,試根據(1)的結論預測該批空調使用年限的最大值.
參考公式:最小二乘估計線性回歸方程![]() 中系數計算公式:
中系數計算公式:
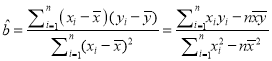 ,
, ![]() ,其中
,其中![]() 表示樣本均值.
表示樣本均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產甲、乙兩種桶裝產品.已知生產甲產品1桶需耗![]() 原料1千克、
原料1千克、![]() 原料2千克;生產乙產品1桶需耗
原料2千克;生產乙產品1桶需耗![]() 原料2千克,
原料2千克, ![]() 原料1千克.每桶甲產品的利潤是300元,每桶乙產品的利潤是400元.公司在生產這兩種產品的計劃中,要求每天消耗
原料1千克.每桶甲產品的利潤是300元,每桶乙產品的利潤是400元.公司在生產這兩種產品的計劃中,要求每天消耗![]() 原料都不超過12千克.通過合理安排生產計劃,從每天生產的甲、乙兩種產品中,公司共可獲得的最大利潤是__________元.
原料都不超過12千克.通過合理安排生產計劃,從每天生產的甲、乙兩種產品中,公司共可獲得的最大利潤是__________元.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com