【題目】
某學校高一數學興趣小組對學生每周平均體育鍛煉小時數與體育成績優秀（體育成績滿分100分，不低于85分稱優秀）人數之間的關系進行分析研究，他們從本校初二，初三，高一，高二，高三年級各隨機抽取了40名學生，記錄并整理了這些學生周平均體育鍛煉小時數與體育成績優秀人數，得到如下數據表：
初二 | 初三 | 高一 | 高二 | 高三 | |
周平均體育鍛煉小時數工（單位：小時） | 14 | 11 | 13 | 12 | 9 |
體育成績優秀人數y（單位：人） | 35 | 26 | 32 | 26 | 19 |
該興趣小組確定的研究方案是：先從這5組數據中選取3組數據求線性回歸方程，再用剩下的2組數據進行檢驗.
（1）若選取的是初三，高一，高二的3組數據，請根據這3組數據，求出y關于x的線性回歸方程
；
（2）若由線性回歸方程得到的估計數據與所選取的檢驗數據的誤差均不超過1，則認為得到的線性回歸方程是可靠的，試問（1）中所得到的線性回歸方程是否可靠？
參考數據：
，
.
參考公式：
，
.
科目：高中數學 來源： 題型：
【題目】某品牌餐飲公司準備在10個規模相當的地區開設加盟店，為合理安排各地區加盟店的個數，先在其中5個地區試點，得到試點地區加盟店個數分別為1，2，3，4，5時，單店日平均營業額
（萬元）的數據如下：
加盟店個數 | 1 | 2 | 3 | 4 | 5 |
單店日平均營業額 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
（1）求單店日平均營業額（萬元）與所在地區加盟店個數
（個）的線性回歸方程；
（2）根據試點調研結果，為保證規模和效益，在其他5個地區，該公司要求同一地區所有加盟店的日平均營業額預計值總和不低于35萬元，求一個地區開設加盟店個數
的所有可能取值；
（3）小趙與小王都準備加入該公司的加盟店，根據公司規定，他們只能分別從其他五個地區（加盟店都不少于2個）中隨機選一個地區加入，求他們選取的地區相同的概率.
（參考數據及公式：
，
，線性回歸方程
，其中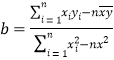
，
.）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
，
是異面直線，
是，外的一點，則下列結論中正確的是（ ）
A.過有且只有一條直線與，都垂直B.過有且只有一條直線與，都平行
C.過有且只有一個平面與，都垂直D.過有且只有一個平面與，都平行
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=aex圖象在x=0處的切線與函數g（x）=lnx圖象在x=1處的切線互相平行．
（Ⅰ）求a的值；
（Ⅱ）設直線x=t（t＞0）分別與曲線y=f（x）和y=g（x）交于P，Q兩點，求證：|PQ|＞2．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知雙曲線
＝1(a＞0，b＞0)的左、右焦點分別為F1，F2，點O為雙曲線的中心，點P在雙曲線右支上，△PF1F2內切圓的圓心為Q，圓Q與x軸相切于點A，過F2作直線PQ的垂線，垂足為B，則下列結論成立的是( )
A. |OA|＞|OB|B. |OA|＜|OB|
C. |OA|＝|OB|D. |OA|與|OB|大小關系不確定
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C的圓心在x軸上，且經過點
．
（1）求圓C的方程；
（2）若點
，直線l平行于OQ（O為坐標原點）且與圓C相交于M，N兩點，直線QM、QN的斜率分別為kQM、kQN，求證：kQM+kQN為定值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
