
 .
. ,求曲線
,求曲線 在點
在點 處的切線方程;
處的切線方程; 在其定義域內為增函數,求正實數
在其定義域內為增函數,求正實數 的取值范圍;
的取值范圍; ,若在
,若在 上至少存在一點
上至少存在一點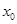 ,使得
,使得 >
> 成立,求實數
成立,求實數 的取值范圍.
的取值范圍. ;(2)實數
;(2)實數 的取值范圍是
的取值范圍是 ;(3)實數
;(3)實數 的取值范圍
的取值范圍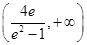 .
. 的導數,找出
的導數,找出 處的導數即切線的斜率,由點斜式列出直線的方程即可;(2)求出函數的定義域,在定義域內利用導數與函數增減性的關系,轉化為恒成立問題進行求解即可;(3)討論
處的導數即切線的斜率,由點斜式列出直線的方程即可;(2)求出函數的定義域,在定義域內利用導數與函數增減性的關系,轉化為恒成立問題進行求解即可;(3)討論 在定義域上的最值,分情況討論
在定義域上的最值,分情況討論 的增減性,進而解決
的增減性,進而解決 存在成立的問題即可.
存在成立的問題即可. 時,函數
時,函數 ,
,
 ,曲線
,曲線 在點
在點 處的切線的斜率為
處的切線的斜率為
 在點
在點 處的切線方程為
處的切線方程為 ,即
,即 3分
3分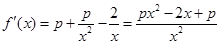
 ,要使
,要使 在定義域
在定義域 內是增函數,只需
內是增函數,只需 在
在 內恒成立
內恒成立 ,
, 的圖象為開口向上的拋物線,對稱軸方程為
的圖象為開口向上的拋物線,對稱軸方程為
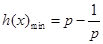 , 只需
, 只需 ,即
,即 時,
時,
 在
在 內為增函數,正實數
內為增函數,正實數 的取值范圍是
的取值范圍是 7分
7分 在
在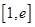 上是減函數
上是減函數 時,
時, ;
;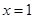 時,
時, ,即
,即
 時,
時, ,其圖象為開口向下的拋物線,對稱軸
,其圖象為開口向下的拋物線,對稱軸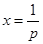 在
在 軸的左側,且
軸的左側,且 ,所以
,所以 在
在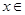
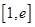 內是減函數
內是減函數 時,
時, ,因為
,因為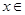
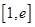 ,所以
,所以 ,
,
 在
在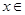
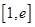 內是減函數
內是減函數 時,
時, 在
在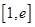 上單調遞減
上單調遞減 ,不合題意
,不合題意 時,由
時,由 ,所以
,所以
 時,
時, 在
在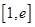 上是增函數
上是增函數 ,不合題意 12分
,不合題意 12分 時,由(Ⅱ)知
時,由(Ⅱ)知 在
在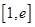 上是增函數,
上是增函數,
 在
在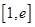 上是減函數,故只需
上是減函數,故只需 ,
,
 ,
,
 ,解得
,解得
 的取值范圍是
的取值范圍是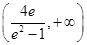 15分.
15分.

 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com