Question

【題目】已知橢圓C： （a＞b＞0）過點（1， ），離心率為 ，過橢圓右頂點A的兩條斜率乘積為﹣ 的直線分別交橢圓C于M，N兩點．
（1）求橢圓C的標準方程；
（2）直線MN是否過定點D？若過定點D，求出點D的坐標；若不過，請說明理由．

Answer 1

【答案】
（1）解：由已知 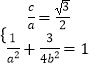，∴a=2，b=1，

∴橢圓C的標準方程為 ；

（2）解：直線MN過定點D（0，0）．

證明如下：由題意，A（2，0），直線AM和直線AN的斜率存在且不為0，

設AM的方程為y=k（x﹣2），代入橢圓方程得（1+4k2）x2﹣16k2x+16k2﹣4=0

∴2xM= ，

∴xM= ，

∴yM=k（xM﹣2）= ，

∴M（ ， ），

∵橢圓右頂點A的兩條斜率乘積為﹣ 的直線分別交橢圓C于M，N兩點，

∴設直線AN的方程為y=﹣ （x﹣2），

同理可得N（ ， ），

xM≠xN，即k 時，kMN= ，

∴直線MN的方程為y﹣ = （x﹣ ），即y= x，

∴直線MN過定點D（0，0）．

xM=xN，即k= 時，直線MN過定點D（0，0）．

綜上所述，直線MN過定點D（0，0）

【解析】（1）由橢圓C： （a＞b＞0）過點（1， ），離心率為 ，建立方程，求出a，b，即可求橢圓C的標準方程；（2）設AM、AN的方程，代入橢圓方程，求出M，N的坐標，進而可得MN的方程，即可得出結論．