
已知圓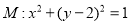 ,設(shè)點
,設(shè)點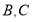 是直線
是直線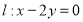 上的兩點,它們的橫坐標(biāo)分別是
上的兩點,它們的橫坐標(biāo)分別是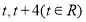 ,點
,點 在線段
在線段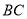 上,過
上,過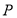 點作圓
點作圓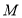 的切線
的切線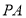 ,切點為
,切點為 .
.
(1)若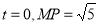 ,求直線
,求直線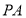 的方程;
的方程;
(2)經(jīng)過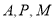 三點的圓的圓心是
三點的圓的圓心是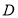 ,求線段
,求線段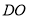 (
(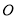 為坐標(biāo)原點)長的最小值
為坐標(biāo)原點)長的最小值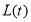 .
.
(1)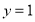 或
或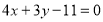 ;(2)
;(2) .
.
【解析】
試題分析:(1)因為點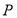 在線段
在線段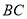 上,所以可假設(shè)點
上,所以可假設(shè)點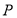 的坐標(biāo),又根據(jù)
的坐標(biāo),又根據(jù)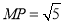 ,所以可求出點
,所以可求出點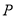 的坐標(biāo),同時要檢驗一下使得點
的坐標(biāo),同時要檢驗一下使得點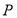 符合在線段
符合在線段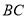 上,再通過假設(shè)直線的斜率,利用點到直線的距離等于圓的半徑即可求出直線的斜率,從而得到切線方程;(2)因為經(jīng)過
上,再通過假設(shè)直線的斜率,利用點到直線的距離等于圓的半徑即可求出直線的斜率,從而得到切線方程;(2)因為經(jīng)過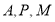 三點的圓的圓心是
三點的圓的圓心是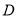 ,求線段
,求線段 (
( 為坐標(biāo)原點)長,通過假設(shè)點
為坐標(biāo)原點)長,通過假設(shè)點 的坐標(biāo)即可表示線段
的坐標(biāo)即可表示線段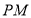 的中點
的中點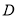 的坐標(biāo)(因為
的坐標(biāo)(因為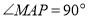 ), 根據(jù)兩點間的距離公式寫出
), 根據(jù)兩點間的距離公式寫出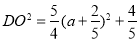 的表達(dá)式,接著關(guān)鍵是根據(jù)
的表達(dá)式,接著關(guān)鍵是根據(jù) 的范圍討論,因為
的范圍討論,因為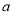 的值受
的值受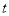 的大小決定的,要分三種情況討論即i)
的大小決定的,要分三種情況討論即i) 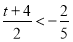 ;ii)
;ii) 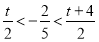 ;iii)
;iii) 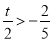 ;分別求出三種情況的最小值即為所求的結(jié)論.
;分別求出三種情況的最小值即為所求的結(jié)論.
試題解析:(1)設(shè)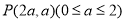

解得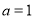 或
或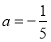 (舍去)
(舍去)
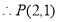
由題意知切線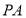 的斜率存在,設(shè)斜率為
的斜率存在,設(shè)斜率為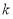
所以直線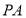 的方程為
的方程為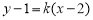 ,即
,即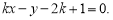
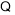 直線
直線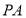 與圓
與圓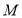 相切,
相切,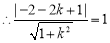 ,解得
,解得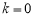 或
或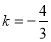
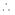 直線
直線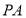 的方程是
的方程是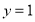 或
或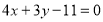 6分
6分
(2)設(shè)
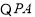 與圓
與圓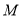 相切于點
相切于點

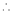 經(jīng)過
經(jīng)過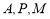 三點的圓的圓心
三點的圓的圓心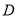 是線段
是線段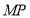 的中點
的中點
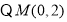
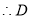 的坐標(biāo)是
的坐標(biāo)是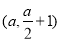
設(shè)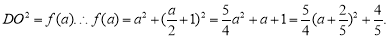
當(dāng)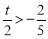 ,即
,即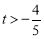 時,
時,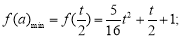
當(dāng)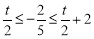 ,即
,即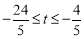 時,
時,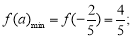
當(dāng)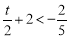 ,即
,即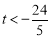 時,
時,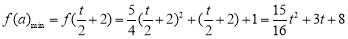
則 .
.
考點:1.直線與圓的位置關(guān)系;2.點到直線的距離公式;3.動區(qū)間的二次函數(shù)的最值問題;4.分類討論的思想.


科目:高中數(shù)學(xué) 來源:2016屆江蘇常州市高一上學(xué)期期末考試數(shù)學(xué)試卷(解析版) 題型:填空題
已知向量 ,若
,若 ,則實數(shù)
,則實數(shù) = .
= .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2016屆江蘇南京第三中學(xué)高一上期中考試數(shù)學(xué)試卷(解析版) 題型:填空題
已知函數(shù)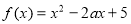 (
(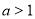 ),若
),若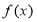 的定義域和值域均是
的定義域和值域均是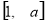 ,則實數(shù)
,則實數(shù)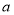 =
=
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2016屆江蘇南京第三中學(xué)高一上期中考試數(shù)學(xué)試卷(解析版) 題型:填空題
已知 是奇函數(shù),當(dāng)
是奇函數(shù),當(dāng) 時,
時, ,則
,則 _____________
_____________
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2016屆廣西桂林十八中高一下學(xué)期開學(xué)考數(shù)學(xué)試卷(解析版) 題型:選擇題
把正方形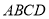 沿對角線
沿對角線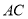 折起,當(dāng)以
折起,當(dāng)以 四點為頂點的三棱錐體積最大時,直線
四點為頂點的三棱錐體積最大時,直線 和平面
和平面 所成的角的大小為( )
所成的角的大小為( )
A. B.
B.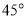 C.
C.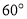 D.
D.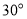
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2016屆廣東省高一上學(xué)期期中考試數(shù)學(xué)試卷(解析版) 題型:填空題
函數(shù)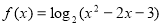 的單調(diào)遞增區(qū)間為 .
的單調(diào)遞增區(qū)間為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2016屆廣東省高一上學(xué)期期中模塊考試數(shù)學(xué)試卷(解析版) 題型:填空題
若直線 與曲線
與曲線 有四個交點,則實數(shù)
有四個交點,則實數(shù) 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com