
【題目】如圖,在四棱柱 ![]() 中,側(cè)面
中,側(cè)面![]() 和側(cè)面
和側(cè)面![]() 都是矩形,
都是矩形, ![]() 是邊長(zhǎng)為
是邊長(zhǎng)為![]() 的正三角形,
的正三角形, ![]() 分別為
分別為![]() 的中點(diǎn).
的中點(diǎn).
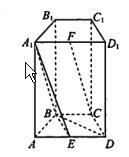
(1)求證: ![]() 平面
平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() .
.
(3)若![]() 平面
平面![]() ,求棱
,求棱![]() 的長(zhǎng)度.
的長(zhǎng)度.
【答案】(1)詳見解析; (2)詳見解析; (3)1.
【解析】試題分析:(1)本問(wèn)考查線面垂直的證明,根據(jù)線面垂直判定定理可知,應(yīng)證明![]() 與平面ABCD內(nèi)的兩條相交直線垂直,根據(jù)已知條件側(cè)面
與平面ABCD內(nèi)的兩條相交直線垂直,根據(jù)已知條件側(cè)面![]() 和側(cè)面
和側(cè)面![]() 都是矩形,所以
都是矩形,所以![]() ,且
,且![]() ,于是問(wèn)題得證;(2)本問(wèn)考查面面垂直的證明,應(yīng)先證明線面垂直,根據(jù)題中條件
,于是問(wèn)題得證;(2)本問(wèn)考查面面垂直的證明,應(yīng)先證明線面垂直,根據(jù)題中條件![]() 為正三角形,E為AD中點(diǎn),所以BE
為正三角形,E為AD中點(diǎn),所以BE![]() AD,根據(jù)面面垂直的性質(zhì)定理,則BE
AD,根據(jù)面面垂直的性質(zhì)定理,則BE![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以問(wèn)題得證;(3)本問(wèn)考查線面平行的性質(zhì)定理,確定經(jīng)過(guò)CF的平面與平面
,所以問(wèn)題得證;(3)本問(wèn)考查線面平行的性質(zhì)定理,確定經(jīng)過(guò)CF的平面與平面![]() 的交線,從而得到CF平行于交線,然后根據(jù)平面幾何知識(shí)求BC的長(zhǎng)度.
的交線,從而得到CF平行于交線,然后根據(jù)平面幾何知識(shí)求BC的長(zhǎng)度.
試題解析:(1)因?yàn)閭?cè)面![]() 和側(cè)面
和側(cè)面![]() 都是矩形,所以
都是矩形,所以![]() ,且
,且![]() .因?yàn)?/span>
.因?yàn)?/span>![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)因?yàn)?/span>![]() 是正三角形,且
是正三角形,且![]() 為
為![]() 中點(diǎn),所以
中點(diǎn),所以![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() .因?yàn)?/span>
.因?yàn)?/span>![]() ,所以
,所以![]() 平面
平面![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(3)因?yàn)?/span>![]() ,而
,而![]() 為
為![]() 的中點(diǎn),所以
的中點(diǎn),所以![]() ,所以
,所以![]() 四點(diǎn)共面.因?yàn)?/span>
四點(diǎn)共面.因?yàn)?/span>![]() 平面
平面![]() ,而平面
,而平面![]() 平面
平面![]() ,所以
,所以![]() .所以四邊形
.所以四邊形![]() 是平行四邊形.所以
是平行四邊形.所以![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知數(shù)列![]() 滿足
滿足![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 為非零常數(shù).
為非零常數(shù).
(1)若![]() ,
, ![]() ,求證:
,求證: ![]() 為等比數(shù)列,并求數(shù)列
為等比數(shù)列,并求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)若數(shù)列![]() 是公差不等于零的等差數(shù)列.
是公差不等于零的等差數(shù)列.
①求實(shí)數(shù)![]() ,
, ![]() 的值;
的值;
②數(shù)列![]() 的前
的前![]() 項(xiàng)和
項(xiàng)和![]() 構(gòu)成數(shù)列
構(gòu)成數(shù)列![]() ,從
,從![]() 中取不同的四項(xiàng)按從小到大排列組成四項(xiàng)子數(shù)列.試問(wèn):是否存在首項(xiàng)為
中取不同的四項(xiàng)按從小到大排列組成四項(xiàng)子數(shù)列.試問(wèn):是否存在首項(xiàng)為![]() 的四項(xiàng)子數(shù)列,使得該子數(shù)列中的所有項(xiàng)之和恰好為2017?若存在,求出所有滿足條件的四項(xiàng)子數(shù)列;若不存在,請(qǐng)說(shuō)明理由.
的四項(xiàng)子數(shù)列,使得該子數(shù)列中的所有項(xiàng)之和恰好為2017?若存在,求出所有滿足條件的四項(xiàng)子數(shù)列;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,點(diǎn)A是以線段BC為直徑的圓O上一點(diǎn),AD⊥BC于點(diǎn)D,過(guò)點(diǎn)B作圓O的切線,與CA的延長(zhǎng)線相交于點(diǎn)E,點(diǎn)G是AD的中點(diǎn),連接CG并延長(zhǎng)與BE相交于點(diǎn)F,延長(zhǎng)AF與CB的延長(zhǎng)線相交于點(diǎn)P. 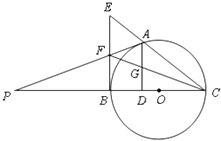
(1)求證:BF=EF;
(2)求證:PA是圓O的切線.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知公差不為0的等差數(shù)列{an}的前n項(xiàng)和為Sn, S3=a4+6,且a1, a4, a13成等比數(shù)列.
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)設(shè)![]() ,求數(shù)列{bn}的前n項(xiàng)和.
,求數(shù)列{bn}的前n項(xiàng)和.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】首屆世界低碳經(jīng)濟(jì)大會(huì)在南昌召開,本屆大會(huì)以“節(jié)能減排,綠色生態(tài)”為主題,某單位在國(guó)家科研部門的支持下,進(jìn)行技術(shù)攻關(guān),采用了新式藝,把二氧化碳轉(zhuǎn)化為一種可利用的化工產(chǎn)品,已知該單位每月的處理量最少為300噸,最多為600噸,月處理成本![]() (元)與月處理量
(元)與月處理量![]() (噸)之間的函數(shù)關(guān)系可近似地表示為
(噸)之間的函數(shù)關(guān)系可近似地表示為![]() ,且每處理一噸二氧化碳得到可利用的化工產(chǎn)品價(jià)值為200元.
,且每處理一噸二氧化碳得到可利用的化工產(chǎn)品價(jià)值為200元.
(1)該單位每月處理量為多少噸時(shí),才能使每噸的平均處理成本最低?
(2)該單位每月能否獲利?如果獲利,求出最大利潤(rùn);如果不獲利,則需要國(guó)家至少補(bǔ)貼多少元才能使該單位不虧損?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知f(x)是定義在R上的偶函數(shù),當(dāng)x≥0時(shí),f(x)=x2﹣x
(1)求f(x)的解析式;
(2)畫出f(x)的圖象;
(3)若方程f(x)=k有4個(gè)解,求k的范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)集合![]() .如果對(duì)于
.如果對(duì)于![]() 的每一個(gè)含有
的每一個(gè)含有![]() 個(gè)元素的子集
個(gè)元素的子集![]() ,
, ![]() 中必有4個(gè)元素的和等于
中必有4個(gè)元素的和等于![]() ,稱正整數(shù)
,稱正整數(shù)![]() 為集合
為集合![]() 的一個(gè)“相關(guān)數(shù)”.
的一個(gè)“相關(guān)數(shù)”.
(Ⅰ)當(dāng)![]() 時(shí),判斷5和6是否為集合
時(shí),判斷5和6是否為集合![]() 的“相關(guān)數(shù)”,說(shuō)明理由;
的“相關(guān)數(shù)”,說(shuō)明理由;
(Ⅱ)若![]() 為集合
為集合![]() 的“相關(guān)數(shù)”,證明:
的“相關(guān)數(shù)”,證明: ![]() ;
;
(Ⅲ)給定正整數(shù)![]() .求集合
.求集合![]() 的“相關(guān)數(shù)”
的“相關(guān)數(shù)” ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了響應(yīng)教育部頒布的《關(guān)于推進(jìn)中小學(xué)生研學(xué)旅行的意見》,某校計(jì)劃開設(shè)八門研學(xué)旅行課程,并對(duì)全校學(xué)生的選擇意向進(jìn)行調(diào)查(調(diào)查要求全員參與,每個(gè)學(xué)生必須從八門課程中選出唯一一門課程).本次調(diào)查結(jié)果整理成條形圖如下.

上圖中,已知課程![]() 為人文類課程,課程
為人文類課程,課程![]() 為自然科學(xué)類課程.為進(jìn)一步研究學(xué)生選課意向,結(jié)合上面圖表,采取分層抽樣方法從全校抽取
為自然科學(xué)類課程.為進(jìn)一步研究學(xué)生選課意向,結(jié)合上面圖表,采取分層抽樣方法從全校抽取![]() 的學(xué)生作為研究樣本組(以下簡(jiǎn)稱“組M”).
的學(xué)生作為研究樣本組(以下簡(jiǎn)稱“組M”).
(Ⅰ)在“組M”中,選擇人文類課程和自然科學(xué)類課程的人數(shù)各有多少?
(Ⅱ)為參加某地舉辦的自然科學(xué)營(yíng)活動(dòng),從“組M”所有選擇自然科學(xué)類課程的同學(xué)中隨機(jī)抽取4名同學(xué)前往,其中選擇課程F或課程H的同學(xué)參加本次活動(dòng),費(fèi)用為每人1500元,選擇課程G的同學(xué)參加,費(fèi)用為每人2000元.
(ⅰ)設(shè)隨機(jī)變量![]() 表示選出的4名同學(xué)中選擇課程
表示選出的4名同學(xué)中選擇課程![]() 的人數(shù),求隨機(jī)變量
的人數(shù),求隨機(jī)變量![]() 的分布列;
的分布列;
(ⅱ)設(shè)隨機(jī)變量![]() 表示選出的4名同學(xué)參加科學(xué)營(yíng)的費(fèi)用總和,求隨機(jī)變量
表示選出的4名同學(xué)參加科學(xué)營(yíng)的費(fèi)用總和,求隨機(jī)變量![]() 的期望.
的期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=Asin(ωx+α)(A>0,ω>0,﹣ ![]() <α<
<α< ![]() )的最小正周期是π,且當(dāng)x=
)的最小正周期是π,且當(dāng)x= ![]() 時(shí),f(x)取得最大值2.
時(shí),f(x)取得最大值2.
(1)求f(x)的解析式,并作出f(x)在[0,π]上的圖象(要列表);
(2)將函數(shù)f(x)的圖象向右平移m(m>0)個(gè)單位長(zhǎng)度后得到函數(shù)y=g(x)的圖象,且y=g(x)是偶函數(shù),求m的最小值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com