【題目】已知函數
在
處取得極值，且在
處的切線的斜率為
．
(1) 求
的解析式；
(2) 求過點
的切線方程．
【答案】（1）
；（2）
或
.
【解析】試題分析：（1）由函數
在
處取得極值，且在
處的切線的斜率為
，求出導函數，可得
是
的兩根，且
，解方程組即可求得
的值，從而求得
的解析式；（2）設切點，求切線方程，將點
切線方程得到
，解方程可得
，從可得切線斜率，運用點斜式方程，進而得到所求切線的方程.
試題解析：（1）函數f（x）=ax3+bx2+cx的導數為f'（x）=3ax2+2bx+c， 依題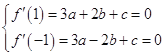
，
又f'（0）=﹣3即c=﹣3 ∴a=1，b=0， ∴f（x）=x3﹣3x
（2）解：設切點為（x0 ， x03﹣3x0）， ∵f'（x）=3x2﹣3∴切線的斜率為f'（x0）=3x02﹣3，∴切線方程為y﹣（x03﹣3x0）=（3x02﹣3）（x﹣x0），
又切線過點A（2，2），
∴2﹣（x03﹣3x0）=（3x02﹣3）（2﹣x0），
∴2x03﹣6x02+8=0，即為2（x0+1）（x0﹣2）2=0， 解得x0=﹣1或2，
可得過點A（2，2）的切線斜率為0或9，
即有過點A（2，2）的切線方程為y﹣2=0或y﹣2=9（x﹣2），
即為y﹣2=0或9x﹣y﹣16=0 .
科目：高中數學 來源： 題型：
【題目】已知集合A＝｛x｜x2－ax＋a2－13＝0｝，B＝｛x｜x2－4x＋3＝0｝，C＝｛x｜x2—3x＝0｝．
（1）若A∩B＝A
B，求a的值；
（2）若
,
求a的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知AB⊥平面ACD，DE∥AB，△ACD是等腰三角形，∠CAD=120°，AD=DE=2AB．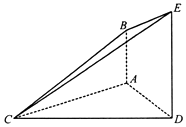 
（I）求證：平面BCE⊥平面CDE；
（II）求平面BCE與平面ADEB所成銳二面角的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系xOy中，圓C的參數方程為
（α為參數），以坐標原點O為極點，以x軸正半軸為極軸，建立極坐標系．
（1）寫出圓C的極坐標方程及圓心C的極坐標；
（2）直線l的極坐標方程為
與圓C交于M，N兩點，求△CMN的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足a1=1，an+1=2an+1（n∈N*）．
（1）求數列{an}的通項公式；
（2）設Sn為數列{ 
}的前n項和，求證：1≤Sn＜4．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=|x+1|﹣2|x﹣a|，a＞0． （Ⅰ）當a=1時，求不等式f（x）＞1的解集；
（Ⅱ）若f（x）的圖象與x軸圍成的三角形面積大于6，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，正方體
的棱長為
, 
分別是棱
，
的中點，過直線
的平面分別與棱
.
交于
，設
，
，給出以下四個命題：
①平面
平面
；②當且僅當
時，四邊形的面積最小； ③四邊形周長
，是單調函數；④四棱錐
的體積
為常函數；
以上命題中真命題的序號為___________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
