
【題目】已知數(shù)列{an}滿足an+1= ![]() ,a1=1,n∈N* .
,a1=1,n∈N* .
(1)求a2 , a3 , a4的值;
(2)求數(shù)列{an}的通項公式.
【答案】
(1)解:∵數(shù)列{an}滿足an+1= ![]() ,a1=1,n∈N*.∴a2=
,a1=1,n∈N*.∴a2= ![]() =
= ![]() ,同理可得:a3=
,同理可得:a3= ![]() ,a4=
,a4= ![]() .
.
(2)解:數(shù)列{an}滿足an+1= ![]() ,a1=1,n∈N*.
,a1=1,n∈N*.
兩邊取倒數(shù)可得: ![]() =
= ![]() +
+ ![]() ,即
,即 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴數(shù)列 ![]() 是等差數(shù)列,首項為1,公差為
是等差數(shù)列,首項為1,公差為 ![]() ,
,
∴ ![]() =1+
=1+ ![]() (n﹣1),解得an=
(n﹣1),解得an= ![]() ,
,
∴an= ![]()
【解析】(1)由數(shù)列{an}滿足an+1= ![]() ,a1=1,n∈N* . 分別令n=1,2,3,即可得出.(2)數(shù)列{an}滿足an+1=
,a1=1,n∈N* . 分別令n=1,2,3,即可得出.(2)數(shù)列{an}滿足an+1= ![]() ,a1=1,n∈N* . 兩邊取倒數(shù)可得:
,a1=1,n∈N* . 兩邊取倒數(shù)可得: ![]() ﹣
﹣ ![]() =
= ![]() ,再利用等差數(shù)列的通項公式即可得出.
,再利用等差數(shù)列的通項公式即可得出.
【考點精析】利用數(shù)列的通項公式對題目進行判斷即可得到答案,需要熟知如果數(shù)列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數(shù)列的通項公式.


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(Ⅰ)若![]() 與
與![]() 在
在![]() 處相切,試求
處相切,試求![]() 的表達式;
的表達式;
(Ⅱ)若![]() 在
在![]() 上是減函數(shù),求實數(shù)
上是減函數(shù),求實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅲ)證明不等式:![]()
![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】寫出下列命題的否定,并判斷其真假:
(1)p:不論m取何實數(shù),方程x2+x-m=0必有實數(shù)根;
(2)q:存在一個實數(shù)x,使得x2+x+1≤0;
(3)r:等圓的面積相等,周長相等.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】小明計劃在8月11日至8月20日期間游覽某主題公園,根據(jù)旅游局統(tǒng)計數(shù)據(jù),該主題公園在此期間“游覽舒適度”(即在園人數(shù)與景區(qū)主管部門核定的最大瞬時容量之比, ![]() 以下為舒適,
以下為舒適, ![]() 為一般,
為一般, ![]() 以上為擁擠),情況如圖所示,小明隨機選擇8月11日至8月19日中的某一天到達該主題公園,并游覽
以上為擁擠),情況如圖所示,小明隨機選擇8月11日至8月19日中的某一天到達該主題公園,并游覽![]() 天.
天.
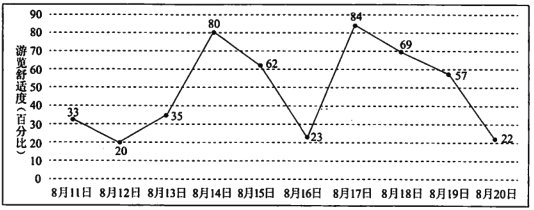
(1)求小明連續(xù)兩天都遇上擁擠的概率;
(2)設![]() 是小明游覽期間遇上舒適的天數(shù),求
是小明游覽期間遇上舒適的天數(shù),求![]() 的分布列和數(shù)學期望;
的分布列和數(shù)學期望;
(3)由圖判斷從哪天開始連續(xù)三天游覽舒適度的方差最大?(結論不要求證明)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某顏料公司生產![]() 兩種產品,其中生產每噸
兩種產品,其中生產每噸![]() 產品,需要甲染料1噸,乙染料4噸,丙染料2噸,生產每噸
產品,需要甲染料1噸,乙染料4噸,丙染料2噸,生產每噸![]() 產品,需要甲染料1噸,乙染料0噸,丙染料5噸,且該公司一條之內甲、乙、丙三種染料的用量分別不超過50噸,160噸和200噸,如果
產品,需要甲染料1噸,乙染料0噸,丙染料5噸,且該公司一條之內甲、乙、丙三種染料的用量分別不超過50噸,160噸和200噸,如果![]() 產品的利潤為300元/噸,
產品的利潤為300元/噸, ![]() 產品的利潤為200元/噸,則該顏料公司一天之內可獲得最大利潤為( )
產品的利潤為200元/噸,則該顏料公司一天之內可獲得最大利潤為( )
A. 14000元 B. 16000元 C. 18000元 D. 20000元
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】用長14.8 m的鋼條制作一個長方體容器的框架,如果所制的底面的一邊比另一邊長0.5 m,那么容器的最大容積為________m3.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某研究性學習小組對春季晝夜溫差大小與某花卉種子發(fā)芽多少之間的關系進行研究,他們分別記錄了3月1日至3月5日的每天晝夜溫差與實驗室每天100顆種子浸泡后的發(fā)芽數(shù),得到如下資料:
K日 日期期 | 1日 | 2日 | 3日 | 4日 | 5日 |
溫差x(℃) | 10 | 11 | 13 | 12 | 8 |
發(fā)芽數(shù)y(顆) | 23 | 25 | 30 | 26 | 16 |
(1)求這5天發(fā)芽數(shù)的中位數(shù);
(2)求這5天的平均發(fā)芽率;
(3)從3月1日至3月5日中任選2天,記前面一天發(fā)芽的種子數(shù)為m,后面一天發(fā)芽的種子數(shù)為n,用(m,n)的形式列出所有基本事件,并求滿足“![]() ”的概率.
”的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com