
【題目】如圖l,在正方形ABCD中,AB=2,E是AB邊的中點,F是BC邊上的一點,對角線AC分別交DE、DF于M、N兩點.將ADAE,CDCF折起,使A、C重合于A點,構成如圖2所示的幾何體.
(I)求證:A′D⊥面A′EF;
(Ⅱ)試探究:在圖1中,F在什么位置時,能使折起后的幾何體中EF∥平面AMN,并給出證明.
【答案】證明:(Ⅰ)∵A′D⊥A′E,A′D⊥A′F,
又A′E∩A′F=A′,A′E面A′EF,A′F面A′EF,
∴A′D⊥面A′EF.
(Ⅱ)當點F為BC的中點時,EF∥面A′MN.
證明如下:當點F為BC的中點時,
在圖(1)中,E,F分別是AB,BC的中點,
所以EF∥AC,
即在圖(2)中有EF∥MN.
又EF面A′MN,MN面A′MN,
所以EF∥面A′MN.
【解析】(Ⅰ)由題意可得,A′D⊥A′E,A′D⊥A′F,A′E∩A′F=A′,利用線面垂直的判定定理即可證得結論;
(Ⅱ)當點F為BC的中點時,EF∥面A′MN.在圖(1)中,E,F分別是AB,BC的中點,可得EF∥AC,而M∈AC,N∈AC,從而可得EF∥MN,繼而有EF∥平面AMN.
【考點精析】根據題目的已知條件,利用直線與平面平行的判定和直線與平面垂直的判定的相關知識可以得到問題的答案,需要掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行;一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想.


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:高中數學 來源: 題型:
【題目】給出下列命題:①定義在![]() 上的函數
上的函數![]() 滿足
滿足![]() ,則
,則![]() 一定不是
一定不是![]() 上的減函數;
上的減函數;
②用反證法證明命題“若實數![]() ,滿足
,滿足![]() ,則
,則![]() 都為0”時,“假設命題的結論不成立”的敘述是“假設
都為0”時,“假設命題的結論不成立”的敘述是“假設![]() 都不為0”;
都不為0”;
③把函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度,所得到的圖象的函數解析式為
個單位長度,所得到的圖象的函數解析式為![]() ;
;
④“![]() ”是“函數
”是“函數![]() 為奇函數”的充分不必要條件.
為奇函數”的充分不必要條件.
其中所有正確命題的序號為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一段時間內,分5次測得某種商品的價格x(萬元)和需求量y(t)之間的一組數據為:
1 | 2 | 3 | 4 | 5 | |
價格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知![]() ,
,
(1)畫出散點圖;
(2)求出y對x的線性回歸方程;
(3)如價格定為1.9萬元,預測需求量大約是多少?(精確到0.01 t).
參考公式: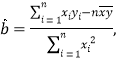
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() ),以原點
),以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若直線![]() 過點
過點![]() ,求直線
,求直線![]() 的極坐標方程;
的極坐標方程;
(2)若直線![]() 與曲線交于
與曲線交于![]() 兩點,求
兩點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的長軸長為4,直線
的長軸長為4,直線![]() 被橢圓
被橢圓![]() 截得的線段長為
截得的線段長為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓![]() 的右頂點作互相垂直的兩條直線
的右頂點作互相垂直的兩條直線![]() 分別交橢圓
分別交橢圓![]() 于
于![]() 兩點(點
兩點(點![]() 不同于橢圓
不同于橢圓![]() 的右頂點),證明:直線
的右頂點),證明:直線![]() 過定點
過定點![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了及時向群眾宣傳“十九大”黨和國家“鄉村振興”戰略,需要尋找一個宣講站,讓群眾能在最短的時間內到宣講站.設有三個鄉鎮,分別位于一個矩形![]() 的兩個頂點
的兩個頂點![]() 及
及![]() 的中點
的中點![]() 處,
處,![]() ,
,![]() ,現要在該矩形的區域內(含邊界),且與
,現要在該矩形的區域內(含邊界),且與![]() 等距離的一點
等距離的一點![]() 處設一個宣講站,記
處設一個宣講站,記![]() 點到三個鄉鎮的距離之和為
點到三個鄉鎮的距離之和為![]() .
.
(Ⅰ)設![]() ,將
,將![]() 表示為
表示為![]() 的函數;
的函數;
(Ⅱ)試利用(Ⅰ)的函數關系式確定宣講站![]() 的位置,使宣講站
的位置,使宣講站![]() 到三個鄉鎮的距離之和
到三個鄉鎮的距離之和![]() 最小.
最小.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在[0,1]上的函數f(x)滿足:
①f(0)=f(1)=0;
②對所有x,y∈[0,1],且x≠y,有|f(x)﹣f(y)|< ![]() |x﹣y|.
|x﹣y|.
若對所有x,y∈[0,1],|f(x)﹣f(y)|<m恒成立,則m的最小值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com