
【題目】設函數f(x)=x2﹣ax+a+3,g(x)=ax﹣2a.
(1)若函數h(x)=f(x)﹣g(x)在[﹣2,0]上有兩個零點,求實數a的取值范圍;
(2)若存在x0∈R,使得f(x0)≤0與g(x0)≤0同時成立,求實數a的最小值.
【答案】
(1)
解:由已知,h(x)=f(x)﹣g(x)=x2﹣2ax+3a+3=0在[﹣2,0]上有兩個不同的實數解,
所以 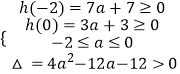 ,
,
即 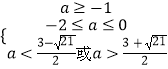 ,
,
解得 ![]() ,
,
(2)
解:由已知, ![]() ,
,
(1)+(2)得 ![]() ,得a≥3,
,得a≥3,
再由(2)得x0≤2,由(1)得 ![]() ,得x0>1,
,得x0>1,
于是,問題等價于:a≥3,且存在x0∈(1,2]滿足 ![]() ,
,
令t=x0﹣1∈(0,1], ![]() ,
,
因為 ![]() 在(0,1]上單調遞減,
在(0,1]上單調遞減,
所以φ(t)≥φ(1)=7,即a≥7,
故實數a的最小值為7.
【解析】(1)由h(x)在區間內的兩個零點,結合圖形,得到需要滿足的條件.(2)由f(x0)≤0與g(x0)≤0同時成立,得到得a≥3,可將問題轉化為最值問題,由單調性得到最值,即可.


科目:高中數學 來源: 題型:
【題目】精準扶貧是鞏固溫飽成果、加快脫貧致富、實現中華民族偉大“中國夢”的重要保障.某地政府在對某鄉鎮企業實施精準扶貧的工作中,準備投入資金將當地農產品進行二次加工后進行推廣促銷,預計該批產品銷售量![]() 萬件(生產量與銷售量相等)與推廣促銷費
萬件(生產量與銷售量相等)與推廣促銷費![]() 萬元之間的函數關系為
萬元之間的函數關系為![]() (其中推廣促銷費不能超過5千元).已知加工此農產品還要投入成本
(其中推廣促銷費不能超過5千元).已知加工此農產品還要投入成本![]() 萬元(不包括推廣促銷費用),若加工后的每件成品的銷售價格定為
萬元(不包括推廣促銷費用),若加工后的每件成品的銷售價格定為![]() 元/件.
元/件.
(1)試將該批產品的利潤![]() 萬元表示為推廣促銷費
萬元表示為推廣促銷費![]() 萬元的函數;(利潤=銷售額-成本-推廣促銷費)
萬元的函數;(利潤=銷售額-成本-推廣促銷費)
(2)當推廣促銷費投入多少萬元時,此批產品的利潤最大?最大利潤為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設圓![]() 的圓心為
的圓心為![]() ,直線
,直線![]() 過點
過點![]() 且與
且與![]() 軸不重合,
軸不重合,![]() 交圓
交圓![]() 于
于![]() 兩點,過
兩點,過![]() 作
作![]() 的平行線交
的平行線交![]() 于點
于點![]() .
.
(1)證明:![]() 為定值,并寫出點
為定值,并寫出點![]() 的軌跡方程;
的軌跡方程;
(2)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() 交
交![]() 于
于![]() 兩點,
兩點,![]() 為坐標原點,求
為坐標原點,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若學生![]() 一天學習數學超過兩個小時的概率為
一天學習數學超過兩個小時的概率為![]() (每天是相互獨立沒有影響的),一周內至少有四天每天學習數學超過兩個小時,就說該生本周數學學習是投入的.
(每天是相互獨立沒有影響的),一周內至少有四天每天學習數學超過兩個小時,就說該生本周數學學習是投入的.
(Ⅰ)①設學生![]() 本周一天學習數學超過兩個小時的天數為
本周一天學習數學超過兩個小時的天數為![]() 求
求![]() 的分布列與數學期望
的分布列與數學期望![]()
②求學生![]() 本周數學學習投入的概率.
本周數學學習投入的概率.
(Ⅱ)為了研究學生學習數學的投入程度和本周數學周練成績的關系,隨機在年級中抽取了![]() 名學生進行調查,所得數據如下表所示:
名學生進行調查,所得數據如下表所示:
成績理想 | 成績不太理想 | 合計 | |
數學學習投入 | 20 | 10 | 30 |
數學學習不太投入 | 10 | 15 | 25 |
合計 | 30 | 25 | 55 |
根據上述數據能否有![]() 的把握認為“學生學習數學的投入程度和本周數學成績兩事件有關”?
的把握認為“學生學習數學的投入程度和本周數學成績兩事件有關”?
附:![]()
|
|
|
|
|
|
|
|
|
|
| 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 對一切實數
對一切實數![]() 都有
都有![]()
![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)已知![]() ,設
,設![]() :當
:當![]() 時,不等式
時,不等式![]() 恒成立;Q:當
恒成立;Q:當![]() 時,
時,![]() 是單調函數。如果滿足
是單調函數。如果滿足![]() 成立的
成立的![]() 的集合記為
的集合記為![]() ,滿足Q成立的
,滿足Q成立的![]() 的集合記為
的集合記為![]() ,求A∩(CRB)(
,求A∩(CRB)(![]() 為全集).
為全集).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P﹣ABCD的底面ABCD為菱形,且∠ABC=60°,
AB=PC=2,PA=PB= ![]() .
.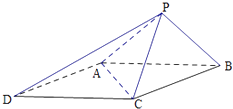
(1)求證:平面PAB⊥平面ABCD;
(2)設H是PB上的動點,求CH與平面PAB所成最大角的正切值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com