【題目】已知圓C：(x＋
)2＋y2＝16，點A(，0)，Q是圓上一動點，AQ的垂直平分線交CQ于點M，設點M的軌跡為E.
(1)求軌跡E的方程；
(2)過點P(1,0)的直線
交軌跡E于兩個不同的點A，B，△AOB(O是坐標原點)的面積S＝
，求直線AB的方程．
【答案】(1) 
＋y2＝1. (2)x＋y－1＝0或x－y－1＝0．
【解析】試題分析：（1）由垂直平分線上的點到兩端點的距離相等，所以|MC|＋|MA|＝|MC|＋|MQ|＝|CQ|＝4>2
，即M點的軌跡是橢圓。（2）由（1）得橢圓方程
＋y2＝1，直線斜率存在，所以設直線方程為x＝my＋1，由面積公式S＝
|OP||y1－y2|＝
及韋達定理可解。
試題解析：(1)由題意|MC|＋|MA|＝|MC|＋|MQ|＝|CQ|＝4>2
，
所以軌跡E是以A，C為焦點，長軸長為4的橢圓，
即軌跡E的方程為
＋y2＝1.
(2)記A(x1，y1)，B(x2，y2)，由題意，直線AB的斜率不可能為0，
而直線x＝1也不滿足條件，故可設AB的方程為x＝my＋1.
由
消去x得(4＋m2)y2＋2my－3＝0，
所以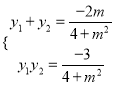 
S＝
|OP||y1－y2|＝
＝
由S＝
，解得m2＝1，即m＝±1.
故直線AB的方程為x＝±y＋1，
即x＋y－1＝0或x－y－1＝0為所求．
科目：高中數學 來源： 題型：
【題目】甲、乙兩地相距500千米，一輛貨車從甲地行駛到乙地，規定速度不得超過100千米
小時.已知貨車每小時的運輸成本(以元為單位)由可變部分和固定部分組成:可變部分與速度
(千米時)的平方成正比，比例系數為0.01；固定部分為
元（
）.
（1）把全程運輸成本
(元)表示為速度(千米時)的函數，并指出這個函數的定義域；
（2）為了使全程運輸成本最小，汽車應以多大速度行駛？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個車間為了規定工時定額，需要確定加工某種零件所花費的時間，為此進行了6次試驗，收集數據如下：
零件數 |
|
|
|
|
|
|
加工時間 |
|
|
|
|
|
|
（Ⅰ）在給定的坐標系中劃出散點圖，并指出兩個變量是正相關還是負相關；
（Ⅱ）求回歸直線方程；
（Ⅲ）試預測加工
個零件所花費的時間？
附：對于一組數據
，
，……，
，其回歸直線
的斜率和截距的最小二乘估計分別為：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
，點
，直線l：
（其中
）．
（Ⅰ）求直線l所經過的定點P的坐標；
（Ⅱ）若分別過A，B且斜率為
的兩條平行直線截直線l所得線段的長為
，求直線
的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知兩條公路
的交匯點
處有一學校，現擬在兩條公路之間的區域內建一工廠
，在兩公路旁
（異于點）處設兩個銷售點，且滿足
，
（千米），
（千米），設
.
（1）試用
表示
，并寫出的范圍；
（2）當為多大時，工廠產生的噪聲對學校的影響最小（即工廠與學校的距離最遠）.
（注：
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在某次測量中得到的A樣本數據如下：52,54,54,56,56,56,55,55,55,55．若B樣本數據恰好是A樣本數據都加6后所得數據，則A，B兩樣本的下列數字特征對應相同的是( )
A. 眾數 B. 平均數
C. 中位數 D. 標準差
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
