
設(shè)a為實(shí)數(shù),設(shè)函數(shù) 的最大值為g(a)。
的最大值為g(a)。
(Ⅰ)設(shè)t= ,求t的取值范圍,并把f(x)表示為t的函數(shù)m(t)
,求t的取值范圍,并把f(x)表示為t的函數(shù)m(t)
(Ⅱ)求g(a)
(Ⅲ)試求滿足 的所有實(shí)數(shù)a
的所有實(shí)數(shù)a
(Ⅰ)m(t)=a(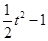 )+t=
)+t=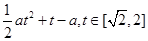
(Ⅱ)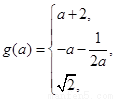

(Ⅲ)滿足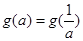 的所有實(shí)數(shù)a為
的所有實(shí)數(shù)a為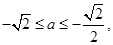 或a=1
或a=1
【解析】解:(Ⅰ)令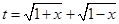
要使有t意義,必須1+x≥0且1-x≥0,即-1≤x≤1,
∴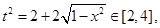 t≥0
①
t≥0
①
t的取值范圍是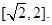 由①得
由①得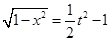
∴m(t)=a(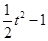 )+t=
)+t=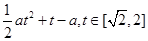
(Ⅱ)由題意知g(a)即為函數(shù)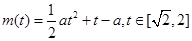 的最大值。
的最大值。
注意到直線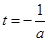 是拋物線
是拋物線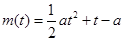 的對(duì)稱軸,分以下幾種情況討論。
的對(duì)稱軸,分以下幾種情況討論。
(1)當(dāng)a>0時(shí),函數(shù)y=m(t), 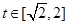 的圖象是開口向上的拋物線的一段,
的圖象是開口向上的拋物線的一段,
由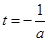 <0知m(t)在
<0知m(t)在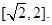 上單調(diào)遞增,∴g(a)=m(2)=a+2
上單調(diào)遞增,∴g(a)=m(2)=a+2
(2)當(dāng)a=0時(shí),m(t)=t, 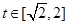 ,∴g(a)=2.
,∴g(a)=2.
(3)當(dāng)a<0時(shí),函數(shù)y=m(t), 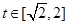 的圖象是開口向下的拋物線的一段,
的圖象是開口向下的拋物線的一段,
若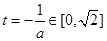 ,即
,即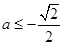 則
則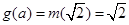
若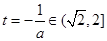 ,即
,即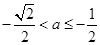 則
則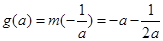
若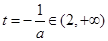 ,即
,即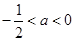 則
則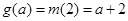
綜上有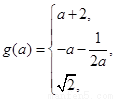
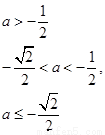
(III)
情形1:當(dāng)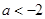 時(shí)
時(shí)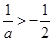 ,此時(shí)
,此時(shí)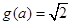 ,
,
由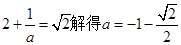 ,與a<-2矛盾。
,與a<-2矛盾。
情形2:當(dāng)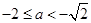
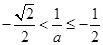 時(shí),此時(shí)
時(shí),此時(shí)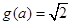 ,
,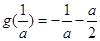
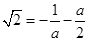 解得,
解得, 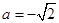 與
與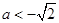 矛盾。
矛盾。
情形3:當(dāng)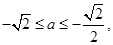
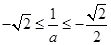 時(shí),此時(shí)
時(shí),此時(shí)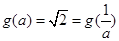
所以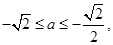
情形4:當(dāng)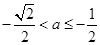 時(shí),
時(shí),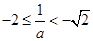 ,此時(shí)
,此時(shí)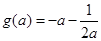 ,
,
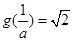
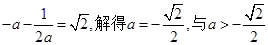 矛盾。
矛盾。
情形5:當(dāng)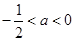 時(shí),
時(shí),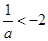 ,此時(shí)g(a)=a+2,
,此時(shí)g(a)=a+2, 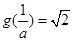
由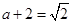 解得
解得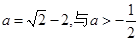 矛盾。
矛盾。
情形6:當(dāng)a>0時(shí),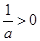 ,此時(shí)g(a)=a+2,
,此時(shí)g(a)=a+2, 
由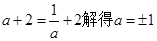 ,由a>0得a=1.
,由a>0得a=1.
綜上知,滿足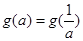 的所有實(shí)數(shù)a為
的所有實(shí)數(shù)a為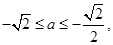 或a=1
或a=1


 課時(shí)訓(xùn)練江蘇人民出版社系列答案
課時(shí)訓(xùn)練江蘇人民出版社系列答案 黃岡經(jīng)典趣味課堂系列答案
黃岡經(jīng)典趣味課堂系列答案 啟東小題作業(yè)本系列答案
啟東小題作業(yè)本系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2009-2010學(xué)年湖南省長沙市同升湖實(shí)驗(yàn)學(xué)校高三(上)第二次月考數(shù)學(xué)試卷(理科)(解析版) 題型:解答題
 的最大值為g(a).
的最大值為g(a). ,求t的取值范圍,并把f(x)表示為t的函數(shù)m(t)
,求t的取值范圍,并把f(x)表示為t的函數(shù)m(t) 的所有實(shí)數(shù)a
的所有實(shí)數(shù)a查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年江蘇省無錫市江陰一中高一(上)第12周數(shù)學(xué)限時(shí)作業(yè)(解析版) 題型:解答題
 的最大值為g(a).
的最大值為g(a). ,求t的取值范圍,并把f(x)表示為t的函數(shù)m(t);
,求t的取值范圍,并把f(x)表示為t的函數(shù)m(t);查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆江西省上饒市、德興一中等高二四校聯(lián)考數(shù)學(xué)試卷 題型:解答題
設(shè)a為實(shí)數(shù),設(shè)函數(shù) 的最大值為g(a)。
的最大值為g(a)。
(Ⅰ)設(shè)t= ,求t的取值范圍,并把f(x)表示為t的函數(shù)m(t)
,求t的取值范圍,并把f(x)表示為t的函數(shù)m(t)
(Ⅱ)求g(a)(Ⅲ)試求滿足 的所有實(shí)數(shù)a
的所有實(shí)數(shù)a
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:江蘇高考真題 題型:解答題
 的最大值為g(a)。
的最大值為g(a)。 ,求t的取值范圍,并把f(x)表示為t的函數(shù)m(t);
,求t的取值范圍,并把f(x)表示為t的函數(shù)m(t); 的所有實(shí)數(shù)a。
的所有實(shí)數(shù)a。查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com