
【題目】如圖,在四面體![]() 中,
中,![]() 分別是線段
分別是線段![]() 的中點,
的中點,![]() ,
,![]() ,
,![]() ,直線
,直線![]() 與平面
與平面![]() 所成的角等于
所成的角等于![]() .
.
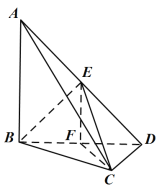
(Ⅰ)證明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)見證明; (Ⅱ) ![]() 。
。
【解析】
(Ⅰ)先證得![]() ,再證得
,再證得![]() ,于是可得
,于是可得![]() 平面
平面![]() ,根據面面垂直的判定定理可得平面
,根據面面垂直的判定定理可得平面![]() 平面
平面![]() .(Ⅱ)利用幾何法求解或建立坐標系,利用向量求解即可得到所求.
.(Ⅱ)利用幾何法求解或建立坐標系,利用向量求解即可得到所求.
(Ⅰ)在![]() 中,
中,![]() 是斜邊
是斜邊![]() 的中點,
的中點,
所以![]() .
.
因為![]() 是
是![]() 的中點,
的中點,
所以![]() ,且
,且![]() ,
,
所以![]() ,
,
所以![]() .
.
又因為![]() ,
,
所以![]() ,
,
又![]() ,
,
所以![]() 平面
平面![]() ,
,
因為![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(Ⅱ)方法一:取![]() 中點
中點![]() ,連
,連![]() ,則
,則![]() ,
,
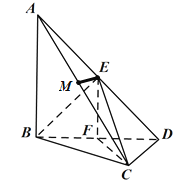
因為![]() ,
,
所以![]() .
.
又因為![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因此![]() 是直線
是直線![]() 與平面
與平面![]() 所成的角.
所成的角.
故![]() ,
,
所以![]() .
.
過點![]() 作
作![]() 于
于![]() ,則
,則![]() 平面
平面![]() ,
,
且![]() .
.
過點![]() 作
作![]() 于
于![]() ,連接
,連接![]() ,
,
則![]() 為二面角
為二面角![]() 的平面角.
的平面角.
因為![]() ,
,
所以![]() ,
,
所以![]() ,
,
因此二面角![]() 的余弦值為
的余弦值為![]() .
.
方法二:
如圖所示,在平面BCD中,作x軸⊥BD,以B為坐標原點,BD,BA所在直線為y軸,z軸建立空間直角坐標系![]() .
.
因為![]() (同方法一,過程略)
(同方法一,過程略)
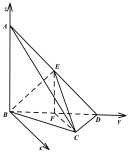
則![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量
的法向量![]() ,
,
則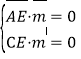 ,即
,即![]() ,取
,取![]() ,得
,得![]() .
.
設平面![]() 的法向量
的法向量![]()
則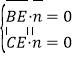 ,即
,即![]() ,取
,取![]() ,得
,得![]() .
.
所以![]() ,
,
由圖形得二面角![]() 為銳角,
為銳角,
因此二面角![]() 的余弦值為
的余弦值為![]() .
.


 新思維假期作業暑假吉林大學出版社系列答案
新思維假期作業暑假吉林大學出版社系列答案科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線 (
(![]() 為參數),曲線
為參數),曲線![]() ,將
,將![]() 的橫坐標伸長為原來的2倍,縱坐標縮短為原來的
的橫坐標伸長為原來的2倍,縱坐標縮短為原來的![]() 得到曲線
得到曲線![]() .
.
(1)求曲線![]() 的普通方程,曲線
的普通方程,曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 為曲線
為曲線![]() 上的任意一點,
上的任意一點,![]() 為曲線
為曲線![]() 上的任意一點,求線段
上的任意一點,求線段![]() 的最小值,并求此時的
的最小值,并求此時的![]() 的坐標;
的坐標;
(3)過(2)中求出的點![]() 做一直線
做一直線![]() ,交曲線
,交曲線![]() 于
于![]() 兩點,求
兩點,求![]() 面積的最大值(
面積的最大值(![]() 為直角坐標系的坐標原點),并求出此時直線
為直角坐標系的坐標原點),并求出此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 滿足如下條件:
滿足如下條件:
①函數![]() 的最小值為
的最小值為![]() ,最大值為9;
,最大值為9;
②![]() 且
且![]() ;
;
③若函數![]() 在區間
在區間![]() 上是單調函數,則
上是單調函數,則![]() 的最大值為2.
的最大值為2.
試探究并解決如下問題:
(Ⅰ)求![]() ,并求
,并求![]() 的值;
的值;
(Ⅱ)求函數![]() 的圖象的對稱軸方程;
的圖象的對稱軸方程;
(Ⅲ)設![]() 是函數
是函數![]() 的零點,求
的零點,求![]() 的值的集合.
的值的集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高三年級有1000人,某次數學考試不同成績段的人數![]() .
.
(1)求該校此次數學考試平均成績;
(2)計算得分超過141的人數;
(3)甲同學每次數學考試進入年級前100名的概率是![]() ,若本學期有4次考試,
,若本學期有4次考試, ![]() 表示進入前100名的次數,寫出
表示進入前100名的次數,寫出![]() 的分布列,并求期望與方差.
的分布列,并求期望與方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列各一元二次不等式中,解集為空集的是( )
A.(x+3)(x﹣1)>0B.(x+4)(x﹣1)<0
C.x2﹣2x+3<0D.2x2﹣3x﹣2>0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設A,B,C,D為平面內的四點,且A(1,3),B(2,–2),C(4,1).
(1)若![]() ,求D點的坐標;
,求D點的坐標;
(2)設向量![]() ,
,![]() ,若k
,若k![]() –
–![]() 與
與![]() +3
+3![]() 平行,求實數
平行,求實數![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com