
【題目】某大型娛樂場有兩種型號的水上摩托,管理人員為了了解水上摩托的使用及給娛樂城帶來的經濟收入情況,對該場所最近6年水上摩托的使用情況進行了統計,得到相關數據如表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代碼 | 1 | 2 | 3 | 4 | 5 | 6 |
使用率 | 11 | 13 | 16 | 15 | 20 | 21 |
(1)請根據以上數據,用最小二乘法求水上摩托使用率![]() 關于年份代碼
關于年份代碼![]() 的線性回歸方程,并預測該娛樂場2018年水上摩托的使用率;
的線性回歸方程,并預測該娛樂場2018年水上摩托的使用率;
(2)隨著生活水平的提高,外出旅游的老百姓越來越多,該娛樂場根據自身的發展需要,準備重新購進一批水上摩托,其型號主要是目前使用的Ⅰ型、Ⅱ型兩種,每輛價格分別為1萬元、1.2萬元.根據以往經驗,每輛水上摩托的使用年限不超過四年.娛樂場管理部對已經淘汰的兩款水上摩托的使用情況分別抽取了50輛進行統計,使用年限如條形圖所示:
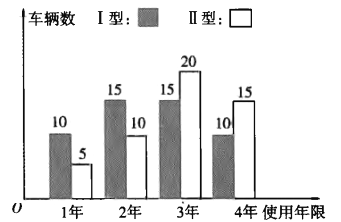
已知每輛水上摩托從購入到淘汰平均年收益是0.8萬元,若用頻率作為概率,以每輛水上摩托純利潤(純利潤![]() 收益
收益![]() 購車成本)的期望值為參考值,則該娛樂場的負責人應該選購Ⅰ型水上摩托還是Ⅱ型水上摩托?
購車成本)的期望值為參考值,則該娛樂場的負責人應該選購Ⅰ型水上摩托還是Ⅱ型水上摩托?
附:回歸直線方程為![]() ,其中
,其中 ,
, ![]() .
.
【答案】(1)回歸方程為![]() .預測該娛樂場2018年水上摩托的使用率為
.預測該娛樂場2018年水上摩托的使用率為![]() .
.
(2)答案見解析.
【解析】試題分析:
(1)由條件所給數據可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,故可求得
,故可求得![]() ,
, ![]() ,所以線性回歸方程為
,所以線性回歸方程為![]() .估計可得當
.估計可得當![]() 時,
時, ![]() ,即2018年水上摩托的使用率為
,即2018年水上摩托的使用率為![]() 。(2)由頻率估計概率,可得每輛Ⅰ型水上摩托可產生的純利潤期望值
。(2)由頻率估計概率,可得每輛Ⅰ型水上摩托可產生的純利潤期望值![]() (萬元),每輛Ⅱ型水上摩托可產生的純利潤期望值
(萬元),每輛Ⅱ型水上摩托可產生的純利潤期望值![]() (萬元),比較可知應該選購Ⅱ型水上摩托。
(萬元),比較可知應該選購Ⅱ型水上摩托。
試題解析:
(1)由表格數據可得![]() ,
, ![]() ,
, ![]() ,
, ![]()
∴
![]() ,
,
∴![]() ,
,
∴水上摩托使用率![]() 關于年份代碼
關于年份代碼![]() 的線性回歸方程為
的線性回歸方程為![]() .
.
當![]() 時,
時, ![]() ,
,
故預測該娛樂場2018年水上摩托的使用率為![]() .
.
(2)由頻率估計概率,結合條形圖知Ⅰ型水上摩托每輛可使用1年、2年、3年和4年的概率分別為0.2,0.3,0.3,0.2,
∴每輛Ⅰ型水上摩托可產生的純利潤期望值
![]() (萬元).
(萬元).
由頻率估計概率,結合條形圖知Ⅱ型水上摩托每輛可使用1年、2年、3年和4年的概率分別為0.1,0.2,0.4和0.3,
∴每輛Ⅱ型水上摩托可產生的純利潤期望值
![]() (萬元).
(萬元).
∵![]() .
.
∴應該選購Ⅱ型水上摩托。


 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若![]() ,函數
,函數![]() 的圖像與函數
的圖像與函數![]() 的圖像相切,求
的圖像相切,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函數
,函數![]() 滿足對任意
滿足對任意![]() ,都有
,都有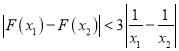 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,函數
,函數![]() ,且
,且![]() 有兩個極值點
有兩個極值點![]() ,其中
,其中![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() 右頂點為
右頂點為![]() ,上頂點為
,上頂點為![]() .已知
.已知![]()
(1)求橢圓的離心率;
(2)設![]() 為橢圓上異于其頂點的一點,以線段
為橢圓上異于其頂點的一點,以線段![]() 為直徑的圓經過點
為直徑的圓經過點![]() 經過點
經過點![]() 的直線
的直線![]() 與該圓相切于點
與該圓相切于點![]() 求橢圓的方程.
求橢圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人進行射擊比賽,各射擊![]() 局,每局射擊
局,每局射擊![]() 次,射擊命中目標得
次,射擊命中目標得![]() 分,未命中目標得
分,未命中目標得![]() 分,兩人
分,兩人![]() 局的得分情況如下:
局的得分情況如下:
甲 |
|
|
|
|
乙 |
|
|
|
|
(Ⅰ)若從甲的![]() 局比賽中,隨機選取
局比賽中,隨機選取![]() 局,求這
局,求這![]() 局的得分恰好相等的概率.
局的得分恰好相等的概率.
(Ⅱ)如果![]() ,從甲、乙兩人的
,從甲、乙兩人的![]() 局比賽中隨機各選取
局比賽中隨機各選取![]() 局,記這
局,記這![]() 局的得分和為
局的得分和為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
(Ⅲ)在![]() 局比賽中,若甲、乙兩人的平均得分相同,且乙的發揮更穩定,寫出
局比賽中,若甲、乙兩人的平均得分相同,且乙的發揮更穩定,寫出![]() 的所有可能取值.(結論不要求證明)
的所有可能取值.(結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個命題:
①將![]() ,
, ![]() ,
, ![]() 三種個體按3:1:2的比例分層抽樣調查,若抽取的
三種個體按3:1:2的比例分層抽樣調查,若抽取的![]() 個體為12個,則樣本容量為30;
個體為12個,則樣本容量為30;
②一組數據1、2、3、4、5的平均數、中位數相同;
③甲組數據的方差為5,乙組數據為5、6、9、10、5,那么這兩組數據中較穩定的是甲;
④統計的10個樣本數據為95,105,114,116,120,120,122,125,130,134,則樣本數據落在![]() 內的頻率為0.4.
內的頻率為0.4.
其中真命題為( )
A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某地區中學生的身體發育狀況,擬采用分層抽樣的方法從甲、乙、丙三所中學抽取![]() 個教學班進行調查.已知甲、乙、丙三所中學分別有
個教學班進行調查.已知甲、乙、丙三所中學分別有![]() ,
, ![]() ,
, ![]() 個教學班.
個教學班.
(Ⅰ)求從甲、乙、丙三所中學中分別抽取的教學班的個數.
(Ⅱ)若從抽取的![]() 個教學班中隨機抽取
個教學班中隨機抽取![]() 個進行調查結果的對比,求這
個進行調查結果的對比,求這![]() 個教學班中至少有一個來自甲學校的概率.
個教學班中至少有一個來自甲學校的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
: ![]() 的長軸長為4,離心率為
的長軸長為4,離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過右焦點![]() 作一條不與坐標軸平行的直線
作一條不與坐標軸平行的直線![]() ,若
,若![]() 交橢圓
交橢圓![]() 與
與![]() 、
、![]() 兩點,點
兩點,點![]() 關于原點
關于原點![]() 的對稱點為
的對稱點為![]() ,求
,求![]() 的面積的取值范圍.
的面積的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com