
【題目】已知![]() .
.
(1)判斷函數![]() 的奇偶性并證明;
的奇偶性并證明;
(2)證明![]() 是定義域內的增函數;
是定義域內的增函數;
(3)解不等式![]() .
.
【答案】(1)奇函數,證明詳見解析;(2)增函數,證明詳見解析;(3)![]() 。
。
【解析】
試題分析:(1)函數![]() 的定義域為R,關于原點對稱,
的定義域為R,關于原點對稱,![]() ,驗證
,驗證![]() 的值,
的值,![]() ,所以即
,所以即![]() ,因此函數
,因此函數![]() 為奇函數;
為奇函數;
(2)首先可以將函數化簡,即![]() ,根據定義證明函數
,根據定義證明函數![]() 在定義域內為增函數,設
在定義域內為增函數,設![]() 是R上任意兩個不等的實數,且
是R上任意兩個不等的實數,且![]() ,則
,則![]() ,
,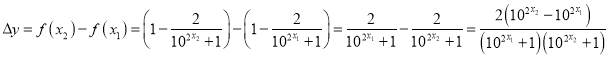 ,由于函數
,由于函數![]() 在R上為增函數,所以當
在R上為增函數,所以當![]() 時,
時,![]() ,則
,則![]() ,
,![]() ,所以
,所以![]() ,則函數
,則函數![]() 在R上為增函數;(3)由第(1)、(2)問可知函數
在R上為增函數;(3)由第(1)、(2)問可知函數![]() 為奇函數且為增函數,所以
為奇函數且為增函數,所以![]() 轉化為
轉化為![]() ,即
,即![]() ,所以轉化為
,所以轉化為![]() ,所以
,所以![]() ,
,![]() ,則
,則![]() 。
。
試題解析:(1)∵![]() 的定義域為R,且
的定義域為R,且![]() ,
,
∴![]() 是奇函數.
是奇函數.
(2)![]()
![]()
![]()
設![]() 且
且![]() ,則
,則
![]()
![]()
![]()
∵![]() 為增函數,∴當
為增函數,∴當![]() 時,
時,![]() ,
,
又∵![]() , ∴
, ∴![]() ,即
,即![]()
∴![]() 在定義域上為增函數.
在定義域上為增函數.
(3) 不等式可化為![]()
由(1)知![]() 是奇函數 ∴
是奇函數 ∴![]()
由(2)知![]() 在定義域上為增函數 ∴
在定義域上為增函數 ∴![]()
解得![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某服裝廠生產一種服裝的成本為40元,出廠單價定為60元,該廠為鼓勵銷售商訂購,決定當一次訂購超過100件時,每多訂購1件,訂購的全部服裝的出場單價就降低0.02元,根據市場調查,銷售商一次訂購量不會超過600件.
(1)設銷售一次訂購![]() 件,服裝的實際出廠單價為
件,服裝的實際出廠單價為![]() 元,寫出函數
元,寫出函數![]() 的表達式;
的表達式;
(2)當銷售商一次訂購多少件服裝時,該廠獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
(1)若![]() ,求函數
,求函數![]() 的表達式;
的表達式;
(2)在(1)的條件下,設函數![]() ,若
,若![]() 上是單調函數,求實數
上是單調函數,求實數![]() 的取值范圍;
的取值范圍;
(3)是否存在![]() 使得函數
使得函數![]() 在
在![]() 上的最大值是4?若存在,求出
上的最大值是4?若存在,求出![]() 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={0,1,2,3},B={x|x(x﹣3)<0},則A∩B=( )
A.{0,1,2,3}
B.{0,1,2}
C.{1,2}
D.{1,2,3}
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com