
(2009山東卷理) (本小題滿分14分)
設橢圓E: ![]() (a,b>0)過M(2,
(a,b>0)過M(2,![]() ) ,N (
) ,N (![]() ,1)兩點,O為坐標原點,
,1)兩點,O為坐標原點,
(I)求橢圓E的方程;
(II)是否存在圓心在原點的圓,使得該圓的任意一條切線與橢圓E恒有兩個交點A,B,且![]() ?若存在,寫出該圓的方程,并求|AB |的取值范圍,若不存在說明理由。
?若存在,寫出該圓的方程,并求|AB |的取值范圍,若不存在說明理由。
![]() ,
,![]()
解:(1)因為橢圓E: ![]() (a,b>0)過M(2,
(a,b>0)過M(2,![]() ) ,N (
) ,N (![]() ,1)兩點,
,1)兩點,
所以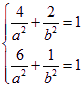 解得
解得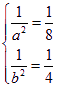 所以
所以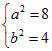 橢圓E的方程為
橢圓E的方程為![]()
(2)假設存在圓心在原點的圓,使得該圓的任意一條切線與橢圓E恒有兩個交點A,B,且![]() ,設該圓的切線方程為
,設該圓的切線方程為![]() 解方程組
解方程組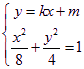 得
得![]() ,即
,即![]() ,
, ![]()
![]()
則△=![]() ,即
,即![]()
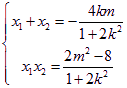 ,
,![]() 要使
要使![]() ,需使
,需使![]() ,即
,即![]() ,所以
,所以![]() ,所以
,所以![]() 又
又![]() ,所以
,所以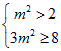 ,所以
,所以![]() ,即
,即![]() 或
或![]() ,因為直線
,因為直線![]() 為圓心在原點的圓的一條切線,所以圓的半徑為
為圓心在原點的圓的一條切線,所以圓的半徑為![]() ,
,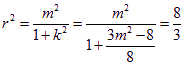 ,
,![]() ,所求的圓為
,所求的圓為![]() ,此時圓的切線
,此時圓的切線![]() 都滿足
都滿足![]() 或
或![]() ,而當切線的斜率不存在時切線為
,而當切線的斜率不存在時切線為![]() 與橢圓
與橢圓![]() 的兩個交點為
的兩個交點為![]() 或
或![]() 滿足
滿足![]() ,綜上, 存在圓心在原點的圓
,綜上, 存在圓心在原點的圓![]() ,使得該圓的任意一條切線與橢圓E恒有兩個交點A,B,且
,使得該圓的任意一條切線與橢圓E恒有兩個交點A,B,且![]() .
.
因為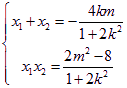 ,
,
所以![]() ,
,
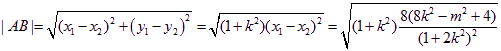
![]() ,
,
①當![]() 時
時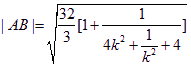
因為![]() 所以
所以 ,
,
所以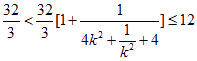 ,
,
所以![]() 當且僅當
當且僅當![]() 時取”=”.
時取”=”. ![]()
![]()
② 當![]() 時,
時,![]() .
.
③ 當AB的斜率不存在時, 兩個交點為![]() 或
或![]() ,
,
所以此時![]() ,
,
綜上, |AB |的取值范圍為![]() 即:
即: ![]()


科目:高中數學 來源: 題型:
(2009山東卷理)(本小題滿分12分)
在某校組織的一次籃球定點投籃訓練中,規定每人最多投3次;在A處每投進一球得3分,在B處每投進一球得2分;如果前兩次得分之和超過3分即停止投籃,否則投第三次,某同學在A處的命中率q![]() 為0.25,在B處的命中率為q
為0.25,在B處的命中率為q![]() ,該同學選擇先在A處投一球,以后都在B處投,用
,該同學選擇先在A處投一球,以后都在B處投,用![]() 表示該同學投籃訓練結束后所得的總分,其分布列為
表示該同學投籃訓練結束后所得的總分,其分布列為
| 0 | 2 | 3 | 4 | 5 |
| 0.03 | P1 | P2 | P3 | P4 |
(1) 求q![]() 的值;
的值; ![]()
![]()
(2) 求隨機變量![]() 的數學期望E
的數學期望E![]() ;
;
(3) 試比較該同學選擇都在B處投籃得分超過3分與選擇上述方式投籃得分超過3分的概率的大小。
查看答案和解析>>
科目:高中數學 來源: 題型:
(2009山東卷理)已知α,β表示兩個不同的平面,m為平面α內的
一條直線,則“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既不充分也不必要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com