
【題目】在平面直角坐標系xOy中,己知圓C經(jīng)過點(![]() ,
,![]() ),(
),(![]() ,
,![]() ),且與直線
),且與直線![]() 相切.
相切.
(1)求圓C的方程;
(2)設P是直線l:x=4上的任意一點,過點P作圓C的切線,切點為M,N.
①求證:直線MN過定點(記為Q);
②設直線PQ與圓C交于點A,B,與y軸交于點D.若![]() ,
,![]() ,求+的值.
,求+的值.
【答案】(1)![]() (2)①證明見解析;②
(2)①證明見解析;②![]()
【解析】
(1)設圓C的方程為![]() ,由此得
,由此得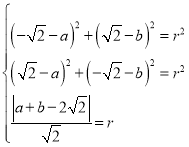 ,解出即可;
,解出即可;
(2)①設P(4,![]() ),由題意P,M,N,C在以PC為直徑的圓
),由題意P,M,N,C在以PC為直徑的圓![]() 上,兩圓方程作差可得直線MN的方程為
上,兩圓方程作差可得直線MN的方程為![]() ,由直線系方程即可求出定點;
,由直線系方程即可求出定點;
②由①得Q(1,0),設直線PQ的方程為![]() ,則D(0,﹣k),設A(
,則D(0,﹣k),設A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),聯(lián)立直線與圓的方程消元,由韋達定理可得
),聯(lián)立直線與圓的方程消元,由韋達定理可得 ,根據(jù)題意可得到
,根據(jù)題意可得到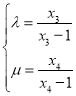 ,代入后化簡求值即可.
,代入后化簡求值即可.
解:(1)設圓C的方程為![]() ,
,
由題意可得,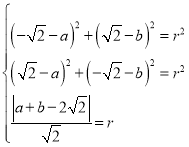 ,
,
解得![]() ,
,![]() ,
,![]() ,
,
∴圓C的方程為![]() ;
;
(2)①設P(4,![]() ),
),
∵PM,PN是圓C的兩條切線,
∴PM⊥MC,PN⊥NC,
∴P,M,N,C在以PC為直徑的圓上,
∴該圓上任意一點![]() 滿足
滿足![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
∴該圓方程為![]() ,
,
由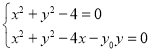 作差可得公共弦所在直線MN的方程為
作差可得公共弦所在直線MN的方程為![]() ,
,
∴直線MN過定點(1,0);
②由①可得Q(1,0),設直線PQ的方程為![]() ,則D(0,﹣k),
,則D(0,﹣k),
設A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
由![]() 得
得![]() ,
,
∴ ,
,
由![]() ,
,![]() ,得
,得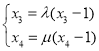 ,即
,即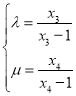 ,
,
∴![]()
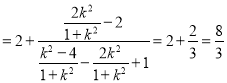 .
.


科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為F,直線l與C交于M,N兩點.
的右焦點為F,直線l與C交于M,N兩點.
(1)若l過點F,點M,N到直線y=2的距離分別為d1,d2,且![]() ,求l的方程;
,求l的方程;
(2)若點M的坐標為(0,1),直線m過點M交C于另一點N′,當直線l與m的斜率之和為2時,證明:直線NN′過定點.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下圖是2020年2月15日至3月2日武漢市新增新冠肺炎確診病例的折線統(tǒng)計圖.則下列說法不正確的是( )

A.2020年2月19日武漢市新增新冠肺炎確診病例大幅下降至三位數(shù)
B.武漢市在新冠肺炎疫情防控中取得了階段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武漢市新增新冠肺炎確診病例低于400人的有8天
D.2020年2月15日到3月2日武漢市新增新冠肺炎確診病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,在直角梯形![]() 中,
中,![]() ,
,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 上的點,
上的點,![]() ,且
,且![]() (如圖①).將四邊形
(如圖①).將四邊形![]() 沿
沿![]() 折起,連接
折起,連接![]() 、
、![]() 、
、![]() (如圖②).在折起的過程中,則下列表述:
(如圖②).在折起的過程中,則下列表述:

①![]() 平面
平面![]() ;
;
②四點![]() 、
、![]() 、
、![]() 、
、![]() 可能共面;
可能共面;
③若![]() ,則平面
,則平面![]() 平面
平面![]() ;
;
④平面![]() 與平面
與平面![]() 可能垂直.其中正確的是__________.
可能垂直.其中正確的是__________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,幾何體是圓柱的一部分,它是由矩形ABCD(及其內部)以AB邊所在直線為旋轉軸旋轉120°得到的,G是![]() 的中點.
的中點.
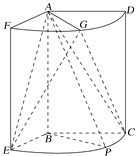
(1)設P是![]() 上的一點,且AP⊥BE,求∠CBP的大小;
上的一點,且AP⊥BE,求∠CBP的大小;
(2)當AB=3,AD=2時,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)![]() sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)為偶函數(shù),且y=f(x)圖象的兩相鄰對稱軸間的距離為
sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)為偶函數(shù),且y=f(x)圖象的兩相鄰對稱軸間的距離為![]() ,則f(
,則f(![]() )的值為( )
)的值為( )
A.﹣1B.1C.![]() .D.
.D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 、
、![]() 中,
中,![]() ,
,![]() ,且
,且![]() ,
,![]() ,設數(shù)列
,設數(shù)列![]() 、
、![]() 的前
的前![]() 項和分別為
項和分別為![]() 和
和![]() .
.
(1)若數(shù)列![]() 是等差數(shù)列,求
是等差數(shù)列,求![]() 和
和![]() ;
;
(2)若數(shù)列![]() 是公比為2的等比數(shù)列.
是公比為2的等比數(shù)列.
①求![]() ;
;
②是否存在實數(shù)![]() ,使
,使![]() 對任意自然數(shù)
對任意自然數(shù)![]() 都成立?若存在,求
都成立?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com