
【題目】我國南北朝時期的數學家祖暅提出了計算體積的祖暅原理:“冪勢既同,則積不容異。”意思是:兩個等高的幾何體若在所有等高處的水平截面的面積相等,則這兩個幾何體的體積相等.已知曲線![]() ,直線
,直線![]() 為曲線
為曲線![]() 在點
在點![]() 處的切線.如圖所示,陰影部分為曲線
處的切線.如圖所示,陰影部分為曲線![]() 、直線
、直線![]() 以及
以及![]() 軸所圍成的平面圖形,記該平面圖形繞
軸所圍成的平面圖形,記該平面圖形繞![]() 軸旋轉一周所得的幾何體為
軸旋轉一周所得的幾何體為![]() .給出以下四個幾何體:
.給出以下四個幾何體:





① ② ③ ④
圖①是底面直徑和高均為![]() 的圓錐;
的圓錐;
圖②是將底面直徑和高均為![]() 的圓柱挖掉一個與圓柱同底等高的倒置圓錐得到的幾何體;
的圓柱挖掉一個與圓柱同底等高的倒置圓錐得到的幾何體;
圖③是底面邊長和高均為![]() 的正四棱錐;
的正四棱錐;
圖④是將上底面直徑為![]() ,下底面直徑為
,下底面直徑為![]() ,高為
,高為![]() 的圓臺挖掉一個底面直徑為
的圓臺挖掉一個底面直徑為![]() ,高為
,高為![]() 的倒置圓錐得到的幾何體.
的倒置圓錐得到的幾何體.
根據祖暅原理,以上四個幾何體中與![]() 的體積相等的是( )
的體積相等的是( )
A. ①B. ②C. ③D. ④
科目:高中數學 來源: 題型:
【題目】已知數列![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
(1)證明:數列![]() 是等比數列,并求數列
是等比數列,并求數列![]() 的通項公式;
的通項公式;
(2)在數列![]() 中,是否存在連續三項成等差數列?若存在,求出所有符合條件的項;若不存在,請說明理由;
中,是否存在連續三項成等差數列?若存在,求出所有符合條件的項;若不存在,請說明理由;
(3)若![]() 且
且![]() ,
,![]() ,求證:使得
,求證:使得![]() ,
,![]() ,
,![]() 成等差數列的點列
成等差數列的點列![]() 在某一直線上.
在某一直線上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠共有男女員工500人,現從中抽取100位員工對他們每月完成合格產品的件數統計如下:
每月完成合格產品的件數(單位:百件) |
|
|
|
|
|
頻數 | 10 | 45 | 35 | 6 | 4 |
男員工人數 | 7 | 23 | 18 | 1 | 1 |
(1)其中每月完成合格產品的件數不少于3200件的員工被評為“生產能手”.由以上統計數據填寫下面![]() 列聯表,并判斷是否有95%的把握認為“生產能手”與性別有關?
列聯表,并判斷是否有95%的把握認為“生產能手”與性別有關?
非“生產能手” | “生產能手” | 合計 | |
男員工 | |||
女員工 | |||
合計 |
(2)為提高員工勞動的積極性,工廠實行累進計件工資制:規定每月完成合格產品的件數在定額2600件以內的,計件單價為1元;超出![]() 件的部分,累進計件單價為1.2元;超出
件的部分,累進計件單價為1.2元;超出![]() 件的部分,累進計件單價為1.3元;超出400件以上的部分,累進計件單價為1.4元.將這4段中各段的頻率視為相應的概率,在該廠男員工中選取1人,女員工中隨機選取2人進行工資調查,設實得計件工資(實得計件工資=定額計件工資+超定額計件工資)不少于3100元的人數為,求的分布列和數學期望.
件的部分,累進計件單價為1.3元;超出400件以上的部分,累進計件單價為1.4元.將這4段中各段的頻率視為相應的概率,在該廠男員工中選取1人,女員工中隨機選取2人進行工資調查,設實得計件工資(實得計件工資=定額計件工資+超定額計件工資)不少于3100元的人數為,求的分布列和數學期望.
附:![]() ,
,
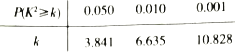 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題p:實數x滿足x2-2ax-3a2<0(a>0),命題q:實數x滿足![]() ≥0.
≥0.
(Ⅰ)若a=1,p,q都為真命題,求x的取值范圍;
(Ⅱ)若q是p的充分不必要條件,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是拋物線
是拋物線![]() 上的一點,拋物線
上的一點,拋物線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知過點![]() 的兩條不重合直線
的兩條不重合直線![]() ,
,![]() 的斜率之積為
的斜率之積為![]() ,且直線
,且直線![]() ,
,![]() 分別交拋物線
分別交拋物線![]() 于
于![]() ,
,![]() 兩點和
兩點和![]() ,
,![]() 兩點.是否存在常數
兩點.是否存在常數![]() 使得
使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,等腰梯形![]() 中
中![]() ,
,![]() ,
,![]() 為
為![]() 的三等分點,以
的三等分點,以![]() 為折痕把△
為折痕把△![]() 折起,使點
折起,使點![]() 到達點
到達點![]() 的位置,且
的位置,且![]() 與平面
與平面![]() 所成角的正切值為
所成角的正切值為![]() .
.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.


查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從一批蘋果中,隨機抽取50個,其重量(單位:克)的頻數分布表如下:
分組(重量) |
|
|
|
|
頻數(個) | 5 | 10 | 20 | 15 |
(1) 根據頻數分布表計算蘋果的重量在![]() 的頻率;
的頻率;
(2) 用分層抽樣的方法從重量在![]() 和
和![]() 的蘋果中共抽取4個,其中重量在
的蘋果中共抽取4個,其中重量在![]() 的有幾個?
的有幾個?
(3) 在(2)中抽出的4個蘋果中,任取2個,求重量在![]() 和
和![]() 中各有1個的概率.
中各有1個的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com