
【題目】已知{an}為等差數(shù)列,公差為d,且0<d<1,a5≠ ![]() (k∈Z),sin2a3+2sina5cosa5=sin2a7 , 函數(shù)f(x)=dsin(wx+4d)(w>0)滿足:在
(k∈Z),sin2a3+2sina5cosa5=sin2a7 , 函數(shù)f(x)=dsin(wx+4d)(w>0)滿足:在 ![]() 上單調且存在
上單調且存在 ![]() ,則w范圍是 .
,則w范圍是 .
【答案】0<w≤ ![]()
【解析】解:∵{an}為等差數(shù)列,公差為d,且0<d<1,a5≠ ![]() (k∈Z), sin2a3+2sina5cosa5=sin2a7 ,
(k∈Z), sin2a3+2sina5cosa5=sin2a7 ,
∴2sina5cosa5=sin2a7﹣sin2a3=2sin ![]() cos
cos ![]() 2cos
2cos ![]() sin
sin ![]() =2sina5cos2d2cosa5sin2d,
=2sina5cos2d2cosa5sin2d,
∴sin4d=1,
∴d= ![]() .
.
∴f(x)= ![]() coswx,
coswx,
∵在 ![]() 上單調且存在
上單調且存在 ![]() ,
,
∴ ![]() ,
,
∴0<w≤ ![]() .
.
所以答案是0<w≤ ![]() .
.
【考點精析】利用等差數(shù)列的性質對題目進行判斷即可得到答案,需要熟知在等差數(shù)列{an}中,從第2項起,每一項是它相鄰二項的等差中項;相隔等距離的項組成的數(shù)列是等差數(shù)列.


科目:高中數(shù)學 來源: 題型:
【題目】將![]() 的圖像向左平移
的圖像向左平移![]() 個單位,再向下平移1個單位,得到函數(shù)
個單位,再向下平移1個單位,得到函數(shù)![]() 的圖像,則下列關于函數(shù)
的圖像,則下列關于函數(shù)![]() 的說法中正確的個數(shù)是( )
的說法中正確的個數(shù)是( )
① 函數(shù)![]() 的最小正周期是
的最小正周期是![]() ② 函數(shù)
② 函數(shù)![]() 的一條對稱軸是
的一條對稱軸是![]()
③函數(shù)![]() 的一個零點是
的一個零點是![]() ④函數(shù)
④函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上單調遞減
上單調遞減
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知點![]() 在拋物線
在拋物線![]()
![]() 上,
上, ![]() 點到拋物線
點到拋物線![]() 的焦點
的焦點![]() 的距離為2,直線
的距離為2,直線
![]()
![]() 與拋物線交于
與拋物線交于![]() 兩點.
兩點.
(1)求拋物線![]() 的方程;
的方程;
(2)若以![]() 為直徑的圓與
為直徑的圓與![]() 軸相切,求該圓的方程.
軸相切,求該圓的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】以原點O為極點,x軸的正半軸為極軸建立極坐標系,直線l的方程為 ![]() ,⊙C的極坐標方程為ρ=4cosθ+2sinθ.
,⊙C的極坐標方程為ρ=4cosθ+2sinθ.
(1)求直線l和⊙C的普通方程;
(2)若直線l與圓⊙C交于A,B兩點,求弦AB的長.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】解答題
(1)求函數(shù)y=2|x﹣1|﹣|x﹣4|的值域;
(2)若不等式2|x﹣1|﹣|x﹣a|≥﹣1在x∈R上恒成立,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知命題![]() :
: ![]() 表示雙曲線,命題
表示雙曲線,命題![]() :
: ![]() 表示橢圓。
表示橢圓。
(1)若命題![]() 與命題
與命題![]() 都為真命題,則
都為真命題,則![]() 是
是![]() 的什么條件?
的什么條件?
(請用簡要過程說明是“充分不必要條件”、“必要不充分條件”、“充要條件”和“既不充分也不必要條件”中的哪一個)
(2)若![]() 為假命題,且
為假命題,且![]() 為真命題,求實數(shù)
為真命題,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某企業(yè)為了解下屬某部門對本企業(yè)職工的服務情況,隨機訪問50名職工,根據(jù)這50名職工對該部門的評分,繪制頻率分布直方圖(如圖所示),其中樣本數(shù)據(jù)分組區(qū)間為![]()

(1)求頻率分布直方圖中![]() 的值;
的值;
(2)估計該企業(yè)的職工對該部門評分不低于80的概率;
(3)從評分在![]() 的受訪職工中,隨機抽取2人,求此2人評分都在
的受訪職工中,隨機抽取2人,求此2人評分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,圓C與x軸相切于點T(2,0),與y軸正半軸相交于兩點M,N(點M在點N的下方),且|MN|=3.
(Ⅰ)求圓C的方程;
(Ⅱ)過點M任作一條直線與橢圓 ![]() 相交于兩點A、B,連接AN、BN,求證:∠ANM=∠BNM.
相交于兩點A、B,連接AN、BN,求證:∠ANM=∠BNM.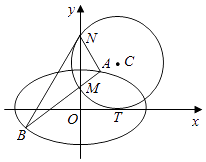
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
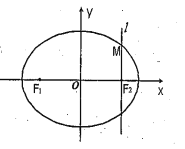
【題目】如圖,在直角坐標![]() 中,設橢圓
中,設橢圓![]()
![]() 的左右兩個焦點分別為
的左右兩個焦點分別為![]() ,過右焦點
,過右焦點![]() 且與
且與![]() 軸垂直的直線
軸垂直的直線![]() 與橢圓
與橢圓![]() 相交,其中一個交點為
相交,其中一個交點為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2>已知![]() 經過點
經過點![]() 且斜率為
且斜率為![]() 直線
直線![]() 與橢圓
與橢圓![]() 有兩個不同的
有兩個不同的![]() 和
和![]() 交點,請問是否存在常數(shù)
交點,請問是否存在常數(shù)![]() ,使得向量
,使得向量![]() 與
與![]() 共線?如果存在,求出
共線?如果存在,求出![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com