Question

【題目】在三棱柱ABC﹣A1B1C1中，已知AB=AC=AA1= ，BC=4，點A1在底面ABC的投影是線段BC的中點O．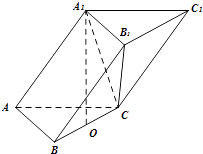

（1）證明在側棱AA1上存在一點E，使得OE⊥平面BB1C1C，并求出AE的長；
（2）求平面A1B1C與平面BB1C1C夾角的余弦值．

Answer 1

【答案】
（1）證明：連接AO，在△AOA1中，作OE⊥AA1于點E，因為AA1∥BB1，所以OE⊥BB1，

因為A1O⊥平面ABC，所以BC⊥平面AA1O，所以BC⊥OE，

所以OE⊥平面BB1C1C，

又AO= =1，AA1= ，

得OE= = = ，

則AE= =

（2）解：如圖，分別以OA，OB，OA1所在直線為x，y，z軸，建立空間直角坐標系，

則A（1，0，0），B（0，2，0），C（0，﹣2，0），A1（0，0，2）

由 ，得點E得坐標是（ ），

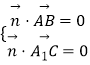設平面A1B1C的法向量是 =（x，y，z），由 得

令y=1，得x=2，z=﹣1，所以 =（2，1，﹣1），

所以cos＜ ， ＞= =

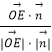即平面A1B1C與平面BB1C1C夾角的余弦值為 ．

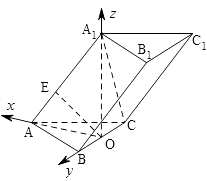
【解析】（1）連接AO，在△AOA1中，作OE⊥AA1于點E，則E為所求．可以證出OE⊥BB1 ， BC⊥OE而得以證明．在RT△A1OA中，利用直角三角形射影定理得出AE．（2）如圖，分別以OA，OB，OA1所在直線為x，y，z軸，建立空間直角坐標系，求出平面A1B1C的法向量是 =（x，y，z），利用 ， 夾角求平面A1B1C與平面BB1C1C夾角的余弦值．
【考點精析】根據題目的已知條件，利用直線與平面垂直的判定的相關知識可以得到問題的答案，需要掌握一條直線與一個平面內的兩條相交直線都垂直，則該直線與此平面垂直；注意點：a)定理中的“兩條相交直線”這一條件不可忽視；b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想．