
【題目】已知函數(shù)f(x)=(1﹣m)lnx+ ![]() ﹣x,m∈R且m≠0.
﹣x,m∈R且m≠0.
(Ⅰ)當(dāng)m=2時(shí),令g(x)=f(x)+log2(3k﹣1),k為常數(shù),求函數(shù)y=g(x)的零點(diǎn)的個(gè)數(shù);
(Ⅱ)若不等式f(x)>1﹣ ![]() 在x∈[1,+∞)上恒成立,求實(shí)數(shù)m的取值范圍.
在x∈[1,+∞)上恒成立,求實(shí)數(shù)m的取值范圍.
【答案】解:(Ⅰ)當(dāng)m=2時(shí),g(x)=﹣lnx+x2﹣x+log2(3k﹣1),x>0,
所以 ![]() ,
,
令g'(x)=0,解得x=1或 ![]() (舍去),
(舍去),
當(dāng)x∈(0,1)時(shí),g'(x)<0,所以y=g(x)在(0,1)上單調(diào)遞減,
當(dāng)x∈(1,+∞)時(shí),g'(x)>0,所以y=g(x)在(1,+∞)上單調(diào)遞增,
所以x=1是y=g(x)的極小值點(diǎn),y=g(x)的最小值為g(1)=log2(3k﹣1)…(3分)
當(dāng)log2(3k﹣1)=0,即 ![]() 時(shí),函數(shù)y=g(x)有一個(gè)零點(diǎn),
時(shí),函數(shù)y=g(x)有一個(gè)零點(diǎn),
當(dāng)log2(3k﹣1)>0,即 ![]() 時(shí),函數(shù)y=g(x)沒有零點(diǎn),
時(shí),函數(shù)y=g(x)沒有零點(diǎn),
當(dāng)log2(3k﹣1)<0,即 ![]() 時(shí),函數(shù)y=g(x)有兩個(gè)零點(diǎn)
時(shí),函數(shù)y=g(x)有兩個(gè)零點(diǎn)
(Ⅱ)由已知  ,
,
令f'(x)=0,解得 ![]() ,由于
,由于 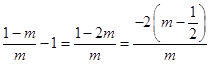 ,
,
①若m<0,則 ![]() ,故當(dāng)x≥1時(shí),f'(x)≤0,因此f(x)在[1,+∞)上單調(diào)遞減,
,故當(dāng)x≥1時(shí),f'(x)≤0,因此f(x)在[1,+∞)上單調(diào)遞減,
所以 ![]() ,又因?yàn)?
,又因?yàn)?![]() ,則
,則 ![]() 不成立
不成立
②若 ![]() ,則
,則 ![]() ,故當(dāng)
,故當(dāng) ![]() 時(shí),f'(x)≤0;當(dāng)
時(shí),f'(x)≤0;當(dāng) ![]() 時(shí),f'(x)>0,
時(shí),f'(x)>0,
即f(x)在 ![]() 上單調(diào)遞減,在
上單調(diào)遞減,在 ![]() 上單調(diào)遞增,
上單調(diào)遞增,
所以  ,
,
因?yàn)?![]() ,所以
,所以 ![]() ,
,
則 ![]() ,
,
因此當(dāng) ![]() 時(shí),
時(shí), ![]() 恒成立
恒成立
③若 ![]() ,則
,則 ![]() ,故當(dāng)x≥1時(shí),f'(x)≥0,
,故當(dāng)x≥1時(shí),f'(x)≥0,
因此f(x)在[1,+∞)上單調(diào)遞增,
故 ![]() ,令
,令 ![]() ,化簡得m2﹣4m+2>0,
,化簡得m2﹣4m+2>0,
解得 ![]() ,所以
,所以 ![]()
綜上所述,實(shí)數(shù)m的取值范圍是 ![]()
【解析】(Ⅰ)求出函數(shù)的導(dǎo)數(shù),解關(guān)于導(dǎo)函數(shù)的不等式,求出函數(shù)的單調(diào)區(qū)間,從而求出函數(shù)的零點(diǎn)個(gè)數(shù)即可;(Ⅱ)求出函數(shù)的導(dǎo)數(shù),通過討論m的范圍,得到函數(shù)的單調(diào)區(qū)間,從而求出函數(shù)f(x)的最小值,確定m的范圍即可.


 陽光考場單元測試卷系列答案
陽光考場單元測試卷系列答案 名校聯(lián)盟沖刺卷系列答案
名校聯(lián)盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=(x+m)lnx,曲線y=f(x)在x=e(e為自然對數(shù)的底數(shù))處得到切線與圓x2+y2=5在點(diǎn)(2,﹣1)處的切線平行.
(1)證明: ![]() ;
;
(2)若不等式(ax+1)(x﹣1)<(a+1)lnx在x∈(0,1)上恒成立,求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】等差數(shù)列{an}的前n項(xiàng)和為Sn , 且a3=9,S6=60.
(I)求數(shù)列{an}的通項(xiàng)公式;
(II)若數(shù)列{bn}滿足bn+1﹣bn=an(n∈N+)且b1=3,求數(shù)列 ![]() 的前n項(xiàng)和Tn .
的前n項(xiàng)和Tn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
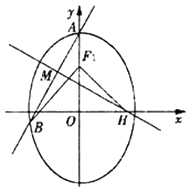
【題目】已知橢圓C: ![]() 的上、下焦點(diǎn)分別為F1 , F2 , 上焦點(diǎn)F1到直線 4x+3y+12=0的距離為3,橢圓C的離心率e=
的上、下焦點(diǎn)分別為F1 , F2 , 上焦點(diǎn)F1到直線 4x+3y+12=0的距離為3,橢圓C的離心率e= ![]() .
. 
(I)若P是橢圓C上任意一點(diǎn),求| ![]() ||
|| ![]() |的取值范圍;
|的取值范圍;
(II)設(shè)過橢圓C的上頂點(diǎn)A的直線l與橢圓交于點(diǎn)B(B不在y軸上),垂直于l的直線與l交于點(diǎn)M,與x軸交于點(diǎn)H,若 ![]() =0,且|
=0,且| ![]() |=|
|=| ![]() |,求直線l的方程.
|,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() sin(2x+
sin(2x+ ![]() )﹣cos2x+
)﹣cos2x+ ![]() .
.
(Ⅰ)求函數(shù)f(x)在[0,π]上的單調(diào)遞增區(qū)間;
(Ⅱ)在△ABC中,a、b、c分別為角A、B、C的對邊,f(A)= ![]() ,a=3,求△ABC面積的最大值.
,a=3,求△ABC面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等差數(shù)列{an}的前n項(xiàng)和為Sn , a1=a,當(dāng)n≥2時(shí), ![]() =3n2an+S
=3n2an+S ![]() ,an≠0,n∈N*.
,an≠0,n∈N*.
(1)求a的值;
(2)設(shè)數(shù)列{cn}的前n項(xiàng)和為Tn , 且cn=3n﹣1+a5 , 求使不等式4Tn>S10成立的最小正整數(shù)n的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 是直線,
是直線,![]() 是平面,給出下列命題:①若
是平面,給出下列命題:①若![]() ,則
,則![]() ;②若
;②若![]() ,則
,則![]() ;③若
;③若![]() 內(nèi)不共線的三點(diǎn)到
內(nèi)不共線的三點(diǎn)到![]() 的距離都相等,則
的距離都相等,則![]() ;④若
;④若![]() ,且
,且![]() ,則
,則![]() ;⑤若
;⑤若![]() 為異面直線,
為異面直線,![]() ,則
,則![]() 。則其中正確的命題是_______.(把你認(rèn)為正確的命題序號都填上)
。則其中正確的命題是_______.(把你認(rèn)為正確的命題序號都填上)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在以A,B,C,D,E,F(xiàn)為頂點(diǎn)的五面體中,面ABEF為正方形,AF=2FD,∠AFD=90°,且二面角D﹣AF﹣E與二面角C﹣BE﹣F都是60°. 
(Ⅰ)證明平面ABEF⊥平面EFDC;
(Ⅱ)求二面角E﹣BC﹣A的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=|x﹣1|﹣2|x+1|的最大值為k.
(1)求k的值;
(2)若a,b,c∈R, ![]() ,求b(a+c)的最大值.
,求b(a+c)的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com