
【題目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(cosα,sinα),設(shè)
=(cosα,sinα),設(shè) ![]() =
= ![]() +t
+t ![]() (t為實數(shù)).
(t為實數(shù)).
(1)若 ![]() ,求當|
,求當| ![]() |取最小值時實數(shù)t的值;
|取最小值時實數(shù)t的值;
(2)若 ![]() ⊥
⊥ ![]() ,問:是否存在實數(shù)t,使得向量
,問:是否存在實數(shù)t,使得向量 ![]() ﹣
﹣ ![]() 和向量
和向量 ![]() 的夾角為
的夾角為 ![]() ,若存在,請求出t;若不存在,請說明理由.
,若存在,請求出t;若不存在,請說明理由.
【答案】
(1)解:因為a= ![]() ,所以
,所以 ![]() =(
=( ![]() ),
), ![]()
![]() =
= ![]() ,
,
則 ![]() =
= ![]() =
= ![]() =
= ![]() =
= 
所以當 ![]() 時,
時, ![]() 取到最小值,最小值為
取到最小值,最小值為 ![]() .
.
(2)解:由條件得cos45°= 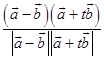 ,
,
又因為 ![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() ,
,
( ![]() )(
)( ![]() )=5﹣t,則有
)=5﹣t,則有 ![]() =
= ![]() ,且t<5,
,且t<5,
整理得t2+5t﹣5=0,所以存在t= ![]() 滿足條件.
滿足條件.
【解析】(1)先把a= ![]() 代入求出向量
代入求出向量 ![]() 的坐標,再把
的坐標,再把 ![]() 轉(zhuǎn)化為
轉(zhuǎn)化為 ![]() =
= ![]() ,把所求結(jié)論以及已知條件代入得到關(guān)于實數(shù)t的二次函數(shù),利用配方法求出
,把所求結(jié)論以及已知條件代入得到關(guān)于實數(shù)t的二次函數(shù),利用配方法求出 ![]() 的最小值以及實數(shù)t的值;(2)先利用向量垂直求出
的最小值以及實數(shù)t的值;(2)先利用向量垂直求出 ![]() 以及
以及 ![]() 和(
和( ![]() )(
)( ![]() ),代入cos45°=
),代入cos45°= 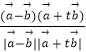 ,可得關(guān)于實數(shù)t的方程,解方程即可求出實數(shù)t.
,可得關(guān)于實數(shù)t的方程,解方程即可求出實數(shù)t.
【考點精析】掌握數(shù)量積表示兩個向量的夾角是解答本題的根本,需要知道設(shè)![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 與
與![]() 的夾角,則
的夾角,則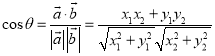 .
.


科目:高中數(shù)學 來源: 題型:
【題目】數(shù)列{an}滿足a1= ![]() ,an+1=a
,an+1=a ![]() ﹣an+1,則M=
﹣an+1,則M= ![]() +
+ ![]() +…+
+…+ ![]() 的整數(shù)部分是( )
的整數(shù)部分是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列{an}的首項為1,Sn為數(shù)列{an}的前n項和,Sn+1=qSn+1,其中q>0,n∈N* .
(1)若2a2 , a3 , a2+2成等差數(shù)列,求數(shù)列{an}的通項公式;
(2)設(shè)數(shù)列{bn}滿足bn= ![]() ,且b2=
,且b2= ![]() ,證明:b1+b2+…+bn>
,證明:b1+b2+…+bn> ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】大學生趙敏利用寒假參加社會實踐,對機械銷售公司7月份至11月份銷售某種機械配件的銷售量及銷售單價進行了調(diào)查,銷售單價x元和銷售量y件之間的一組數(shù)據(jù)如表所示:
月份 | 7 | 8 | 9 | 10 | 11 |
銷售單價x元 | 9 | 9.5 | 10 | 10.5 | 11 |
銷售量y件 | 11 | 10 | 8 | 6 | 5 |
(1)根據(jù)7至11月份的數(shù)據(jù),求出y關(guān)于x的回歸直線方程;
(2)預計在今后的銷售中,銷售量與銷售單價仍然服從(1)中的關(guān)系,若該種機器配件的成本是2.5元/件,那么該配件的銷售單價應定為多少元才能獲得最大利潤? 參考公式:回歸直線方程 ![]() =b
=b ![]() +a,其中b=
+a,其中b= 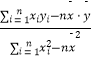 .
.
參考數(shù)據(jù): ![]() =392,
=392, ![]() =502.5.
=502.5.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓C: ![]() ,F(xiàn)1 , F2分別為左右焦點,在橢圓C上滿足條件
,F(xiàn)1 , F2分別為左右焦點,在橢圓C上滿足條件 ![]() 的點A有且只有兩個
的點A有且只有兩個
(1)求橢圓C的方程
(2)若過點F2的兩條相互垂直的直線l1與l2 , 直線l1與曲線y2=4x交于兩點M、N,直線l2與橢圓C交于兩點P、Q,求四邊形PMQN面積的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】![]() .
.
(1)若 ![]() 時,
時, ![]() ,求cos4x的值;
,求cos4x的值;
(2)將 ![]() 的圖象向左移
的圖象向左移 ![]() ,再將各點橫坐標伸長為原來的2倍,縱坐標不變,得y=g(x),若關(guān)于g(x)+m=0在區(qū)間
,再將各點橫坐標伸長為原來的2倍,縱坐標不變,得y=g(x),若關(guān)于g(x)+m=0在區(qū)間 ![]() 上的有且只有一個實數(shù)解,求m的范圍.
上的有且只有一個實數(shù)解,求m的范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知正三角形ABC的邊長為2,AM是邊BC上的高,沿AM將△ABM折起,使得二面角B﹣AM﹣C的大小為90°,此時點M到平面ABC的距離為 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】公元263年左右,我國數(shù)學有劉徽發(fā)現(xiàn)當圓內(nèi)接多邊形的邊數(shù)無限增加時,多邊形的面積可無限逼近圓的面積,并創(chuàng)立了割圓術(shù),利用割圓術(shù)劉徽得到了圓周率精確到小數(shù)點后面兩位的近似值3.14,這就是著名的“徽率”.某同學利用劉徽的“割圓術(shù)”思想設(shè)計了一個計算圓周率的近似值的程序框圖如圖,則輸出S的值為 (參考數(shù)據(jù):sin15°=0.2588,sin7.5°=0.1305)( )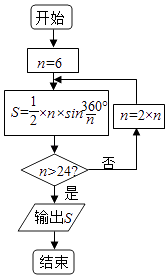
A.2.598
B.3.106
C.3.132
D.3.142
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com