Question

已知長(zhǎng)方體ABCD-A₁B₁C₁D₁中，M、N分別是BB₁和BC的中點(diǎn)，AB=4，AD=2，BB1=2

15

，求異面直線(xiàn)B₁D與MN所成角的余弦值．

Answer 1

分析：連結(jié)B₁C，利用三角形中位線(xiàn)的性質(zhì)得到MN∥B₁C，然后通過(guò)解直角三角形求出三角形DB₁C的三邊，最后利用余弦定理求異面直線(xiàn)B₁D與MN所成角的余弦值．

解答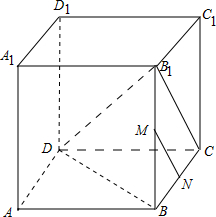：解：如圖：
連結(jié)B₁C，因?yàn)镸，N分別為BB₁和BC的中點(diǎn)，所以MN∥B₁C，
則∠DB₁C為異面直線(xiàn)B₁D與MN所成角．
在直角三角形B₁C₁C中，B1C=

B1C12+CC12

=

22+(2 15 )2

=8．
連結(jié)BD，則BD=

42+22

=2

5

，在直角三角形B₁BD中，B1D=

BD2+BB12

=

(2 5 )2+(2 15 )2

=4

5

．
在三角形DB₁C中，cos∠DB1C=

B1D2+B1C2-DC2

2B1D•B1C

=

(4 5 )2+82-42

2×4 5 ×8

=

2 5

5

．
所以異面直線(xiàn)B₁D與MN所成角的余弦值為

2 5

5

．

點(diǎn)評(píng)：本題考查空間點(diǎn)、線(xiàn)、面的位置關(guān)系及學(xué)生的空間想象能力、求異面直線(xiàn)角的能力．在立體幾何中找平行線(xiàn)是解決問(wèn)題的一個(gè)重要技巧，這個(gè)技巧就是通過(guò)三角形的中位線(xiàn)找平行線(xiàn)，如果試題的已知中涉及到多個(gè)中點(diǎn)，則找中點(diǎn)是出現(xiàn)平行線(xiàn)的關(guān)鍵技巧．