
【題目】已知數(shù)列{an},{bn}的通項(xiàng)公式分別是an=(﹣1)n+2016a,bn=2+ ![]() ,若an<bn , 對任意n∈N+恒成立,則實(shí)數(shù)a的取值范圍是 .
,若an<bn , 對任意n∈N+恒成立,則實(shí)數(shù)a的取值范圍是 .

| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若![]() ,判斷函數(shù)
,判斷函數(shù)![]() 的奇偶性,并加以證明;
的奇偶性,并加以證明;
(2)若函數(shù)![]() 在
在![]() 上是增函數(shù),求實(shí)數(shù)
上是增函數(shù),求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)若存在實(shí)數(shù)![]() 使得關(guān)于
使得關(guān)于![]() 的方程
的方程![]() 有三個不相等的實(shí)數(shù)根,求實(shí)數(shù)
有三個不相等的實(shí)數(shù)根,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
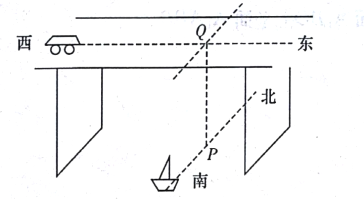
【題目】一只小船以![]() 的速度由南向北勻速駛過湖面,在離湖面高20米的橋上,一輛汽車由西向東以
的速度由南向北勻速駛過湖面,在離湖面高20米的橋上,一輛汽車由西向東以![]() 的速度前進(jìn)(如圖),現(xiàn)在小船在水平面上的
的速度前進(jìn)(如圖),現(xiàn)在小船在水平面上的![]() 點(diǎn)以南的40米處,汽車在橋上
點(diǎn)以南的40米處,汽車在橋上![]() 點(diǎn)以西的30米處(其中
點(diǎn)以西的30米處(其中![]() 水平面),請畫出合適的空間圖形并求小船與汽車間的最短距離.(不考慮汽車與小船本身的大小).
水平面),請畫出合適的空間圖形并求小船與汽車間的最短距離.(不考慮汽車與小船本身的大小).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在(1+x+x2)n= ![]() x
x ![]() x2+…
x2+… ![]() xr+…
xr+… ![]() x2n﹣1
x2n﹣1 ![]() x2n的展開式中,把D
x2n的展開式中,把D ![]() ,D
,D ![]() ,D
,D ![]() …,D
…,D ![]() …,D
…,D ![]() 叫做三項(xiàng)式系數(shù)
叫做三項(xiàng)式系數(shù)
(1)求D ![]() 的值
的值
(2)根據(jù)二項(xiàng)式定理,將等式(1+x)2n=(1+x)n(x+1)n的兩邊分別展開可得,左右兩邊xn的系數(shù)相等,即C ![]() =(C
=(C ![]() )2+(C
)2+(C ![]() )2+(C
)2+(C ![]() )2+…+(C
)2+…+(C ![]() )2 , 利用上述思想方法,請計算D
)2 , 利用上述思想方法,請計算D ![]() C
C ![]() ﹣D
﹣D ![]() C
C ![]() +D
+D ![]() C
C ![]() ﹣…+(﹣1)rD
﹣…+(﹣1)rD ![]() C
C ![]() +..
+.. ![]() C
C ![]() C
C ![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,四棱錐P-ABCD的底面ABCD是邊長為1的菱形,∠BCD=60°,E是CD的中點(diǎn),PA⊥底面ABCD,PA=![]() .
.

(1)證明:平面PBE⊥平面PAB;
(2)求二面角A-BE-P的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,動點(diǎn)P從單位正方形ABCD頂點(diǎn)A開始,順次經(jīng)B、C、D繞邊界一周,當(dāng)![]() 表示點(diǎn)P的行程,
表示點(diǎn)P的行程, ![]() 表示PA之長時,求y關(guān)于x的解析式,并求
表示PA之長時,求y關(guān)于x的解析式,并求![]() 的值.
的值.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
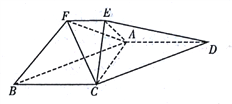
【題目】在如圖所示的幾何體中,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為平行四邊形,
為平行四邊形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求![]() 到平面
到平面![]() 的距離;
的距離;
(3)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)f(x)=﹣4x3+kx,對任意的x∈[﹣1,1],總有f(x)≤1,則實(shí)數(shù)k的取值為 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面ABCD是菱 形,PA=PB,且側(cè)面PAB⊥平面ABCD,點(diǎn)E是AB的中點(diǎn).
中,底面ABCD是菱 形,PA=PB,且側(cè)面PAB⊥平面ABCD,點(diǎn)E是AB的中點(diǎn).
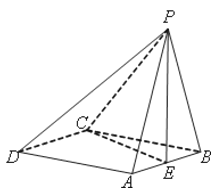
(1)求證:PE⊥AD;
(2)若CA=CB,求證:平面PEC⊥平面PAB.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com