【題目】已知函數
.
（1）若
，則當
時，討論
單調性；
（2）若
，且當
時，不等式
在區間
上有解，求實數
的取值范圍.
【答案】（1）見解析（2）
【解析】試題分析：（1）本問考查利用導數研究函數單調性.首先確定函數
定義域為
，根據題中條件
，然后求導數
，接下來對導數整理得到
，由于
，所以
，且
時， 
或
，然后分別討論
， 
， 
時函數
的單調性；（2）本問主要考查“有解”問題，首先需要將問題等價轉化，即當
時， 
，因此問題轉化為求函數
在區間
上的最大值，由已知條件
，則
，接下來主要考慮分子
，判別式
，分別討論
， 
時函數
的最大值，再根據
即可求出
的取值范圍.
試題解析：（1）
,
,
令
，得
當
時， 
，函數
在定義域
內單調遞減
當
時，在區間
，
在區間
上單調遞增，
當
時，在區間
上
單調遞減，在區間
上
單調遞增，
（2）由題意知，當
時， 
在
上的最大值
,
當
時， 
則
(1) 當
時， 
故
上單調遞增， 
((2))當時
設
的兩根分別為
則
故
綜上，當
時，
所以實數
的取值范圍是
科目：高中數學 來源： 題型：
【題目】如圖，橢圓
的右頂點為
，左、右焦點分別為
、
，過點
且斜率為
的直線與
軸交于點
， 與橢圓交于另一個點
，且點
在
軸上的射影恰好為點
．
（Ⅰ）求橢圓
的標準方程；
（Ⅱ）過點
且斜率大于
的直線與橢圓交于
兩點（
），若
，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某科研機構研發了某種高新科技產品，現已進入實驗階段.已知實驗的啟動資金為10萬元，從實驗的第一天起連續實驗，第
天的實驗需投入實驗費用為
元
，實驗30天共投入實驗費用17700元.
（1）求
的值及平均每天耗資最少時實驗的天數；
（2）現有某知名企業對該項實驗進行贊助，實驗
天共贊助
元
.為了保證產品質量，至少需進行50天實驗，若要求在平均每天實際耗資最小時結束實驗，求
的取值范圍.（實際耗資=啟動資金+試驗費用-贊助費）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有一長為24米的籬笆，一面利用墻(墻最大長度是10米)圍成一個矩形花圃，設該花圃寬AB為x米，面積是y平方米，
(1)求出y關于x的函數解析式，并指出x的取值范圍；
(2)當花圃一邊AB為多少米時，花圃面積最大？并求出這個最大面積？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC﹣A1B1C1中，AA1=AC=2AB=2，且BC1⊥A1C．
（1）求證：平面ABC1⊥平面A1ACC1；
（2）設D是線段BB1的中點，求三棱錐D﹣ABC1的體積．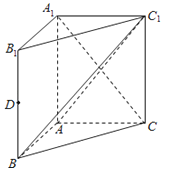
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x），當x，y∈R時，恒有f（x+y）=f（x）+f（y）．當x＞0時，f（x）＞0
（1）求證：f（x）是奇函數；
（2）若
， 試求f（x）在區間[﹣2，6]上的最值；
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
