Question

【題目】某市民用水擬實行階梯水價，每人用水量中不超過立方米的部分按4元/立方米收費，超出立方米的部分按10元/立方米收費，從該市隨機調查了10000位居民，獲得了他們某月的用水量數據，整理得到如下頻率分布直方圖：

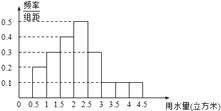
（1）如果為整數，那么根據此次調查，為使80%以上居民在該月的用水價格為4元/立方米， 至少定為多少？

（2）假設同組中的每個數據用該組區間的右端點值代替，當時，估計該市居民該月的人均水費．

Answer 1

【答案】（Ⅰ）3；（Ⅱ）10.5元.

【解析】試題分析：（1）根據水量的頻率分布直方圖知月用水量不超過立方米的居民占，所以至少定為；（2）直接求每個數據用該組區間的右端點值與各組頻率的乘積之和即可.

試題解析：（1）由用水量的頻率分布直方圖知，

該市居民該月用水量在區間內的頻率依次為．

所以該月用水量不超過立方米的居民占，用水量不超過立方米的居民占．依題意， 至少定為

（2）由用水量的頻率分布直方圖及題意，得居民該月用水費用的數據分組與頻率分布表：

組號	1	2	3	4	5	6	7	8
分組
頻率	0.1	0.15	0.2	0.25	0.15	0.05	0.05	0.05

根據題意，該市居民該月的人均水費估計為：

（元）．