
【題目】已知函數f(x)=Asin(ωx+φ)(A,ω>0,﹣π<φ<π)在一個周期內的圖象如圖所示. 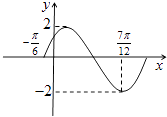
(1)求f(x)的表達式;
(2)在△ABC中,f(C+ ![]() )=﹣1且
)=﹣1且 ![]() <0,求角C.
<0,求角C.
【答案】
(1)解:由圖可知函數的最大值是2,最小值是﹣2,
∴A=2,
∵ ![]() T=
T= ![]() +
+ ![]() =
= ![]() ,
,
∴T=π= ![]() ,可得:ω=2,
,可得:ω=2,
又∵f(x)過點(﹣ ![]() ,0),且根據圖象特征得:﹣2×
,0),且根據圖象特征得:﹣2× ![]() +φ=0+2kπ,k∈Z,
+φ=0+2kπ,k∈Z,
∴φ= ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
而﹣π<φ<π,
∴φ= ![]() .
.
∴f(x)=2sin(2x+ ![]() )
)
(2)解:∵f(x)=2sin(2x+ ![]() ),
),
∴f(C+ ![]() )=2sin(2C
)=2sin(2C ![]() )=﹣1,
)=﹣1,
∴sin(2C ![]() )=﹣
)=﹣ ![]() ,
,
因為C為三角形內角,
∴C= ![]() 或
或 ![]() ,
,
又∵ ![]() =abcosC<0,0<C<π,
=abcosC<0,0<C<π,
∴cosC<0, ![]() <C<π,
<C<π,
∴C= ![]()
【解析】(1)由函數的最值求出A,由周期求出ω,由五點法作圖求出φ的值,從而求得函數f(x)的表達式.(2)利用(1)及f(C+ ![]() )=﹣1可得sin(2C
)=﹣1可得sin(2C ![]() )=﹣
)=﹣ ![]() ,結合角的范圍可求C=
,結合角的范圍可求C= ![]() 或
或 ![]() ,利用平面向量數量積的運算可求cosC<0,從而可求C的值.
,利用平面向量數量積的運算可求cosC<0,從而可求C的值.


科目:高中數學 來源: 題型:
【題目】動點![]() 分別到兩定點
分別到兩定點![]()
![]() 連線的斜率之乘積為
連線的斜率之乘積為![]() ,設
,設![]() 的軌跡為曲線
的軌跡為曲線![]() ,
, ![]() ,
, ![]() 分別為曲線
分別為曲線![]() 的左右焦點,則下列命題中:
的左右焦點,則下列命題中:
(1)曲線![]() 的焦點坐標為
的焦點坐標為![]() ,
, ![]() ;
;
(2)若![]() ,則
,則![]()
![]() ;
;
(3)當![]() 時,
時, ![]() 的內切圓圓心在直線
的內切圓圓心在直線![]() 上;
上;
(4)設![]() ,則
,則![]() 的最小值為
的最小值為![]() .
.
其中正確命題的序號是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱![]() 中,
中, ![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,側棱
,側棱![]() ,
, ![]() 分別為
分別為![]() 與
與![]() 的中點,點
的中點,點![]() 在平面
在平面![]() 上的射影是
上的射影是![]() 的重心.
的重心.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的公差d>0.設{an}的前n項和為Sn,a1=1,S2·S3=36.
(1)求d及Sn;
(2)求m,k(m,k∈N*)的值,使得am+am+1+am+2+…+am+k=65.
查看答案和解析>>
科目:高中數學 來源: 題型:
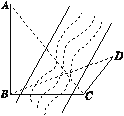
【題目】如圖,為測得河對岸塔AB的高,先在河岸上選一點C,使C在塔底B的正東方向上,測得點A的仰角為60°,再由點C沿北偏東15°方向走10 m到位置D,測得∠BDC=45°,則塔AB的高是( )
A. 10m B. 10![]() m C. 10
m C. 10![]() m D. 10
m D. 10![]() m
m
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() :
: ![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)分別求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設直線![]() 交曲線
交曲線![]() 于
于![]() ,
, ![]() 兩點,交曲線
兩點,交曲線![]() 于
于![]() ,
, ![]() 兩點,求
兩點,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校100名學生期中考試數學成績的頻率分布直方圖如圖:
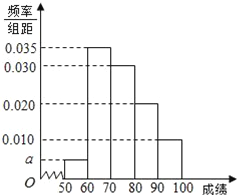
(1)求圖中a的值;
(2)根據頻率分布直方圖,估計這100名學生期中考試數學成績的平均分;
(3)現用分層抽樣的方法從第3、4、5組中隨機抽取6名學生,將該樣本看成一個總體,從中隨機抽取2名,求其中恰有1人的分數不低于90分的概率?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了提高產品的年產量,某企業擬在2013年進行技術改革,經調查測算,產品當年的產量x萬件與投入技術改革費用m萬元(m≥0)滿足x=3﹣ ![]() (k為常數).如果不搞技術改革,則該產品當年的產量只能是1萬件.已知2013年生產該產品的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元.由于市場行情較好,廠家生產均能銷售出去,廠家將每件產品的銷售價格定為每件產品生產成本的1.5倍(生產成本包括固定投入和再投入兩部分資金)
(k為常數).如果不搞技術改革,則該產品當年的產量只能是1萬件.已知2013年生產該產品的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元.由于市場行情較好,廠家生產均能銷售出去,廠家將每件產品的銷售價格定為每件產品生產成本的1.5倍(生產成本包括固定投入和再投入兩部分資金)
(1)試確定k的值,并將2013年該產品的利潤y萬元表示為技術改革費用m萬元的函數(利潤=銷售金額﹣生產成本﹣技術改革費用);
(2)該企業2013年的技術改革費用投入多少萬元時,廠家的利潤最大?并求出最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com