【題目】（1）求
的展開式中
的系數及展開式中各項系數之和；
（2）從0，2，3，4，5，6這6個數字中任取4個組成一個無重復數字的四位數，求滿足條件的四位數的個數.
【答案】（1）
（2）300
【解析】試題分析：（1）直接利用二項展開式定理求解即可展開式中
的系數，令
即可得結果；（2）分選
，不選
兩種情況討論，再利用分類計數加法原理可得結果.
試題解析：（1）∵
，∴展開式中
的系數為
.
令
，得各項系數之和為
.
（2）若不選0，則有
個；
若選0，則有
個.
故能組成
個不同的四位數.
【方法點晴】本題主要考查二項展開式定理的通項與系數及排列組合綜合問題，屬于中檔題題. 二項展開式定理的問題也是高考命題熱點之一，關于二項式定理的命題方向比較明確，主要從以下幾個方面命題：（1）考查二項展開式的通項公式
；（可以考查某一項，也可考查某一項的系數）（2）考查各項系數和和各項的二項式系數和；（3）二項展開式定理的應用.
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分）已知
是定義在
上的奇函數，且
，當
,
時，有
成立．
（Ⅰ）判斷在 上的單調性，并加以證明；
（Ⅱ）若
對所有的
恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列正確命題有__________．
①“
”是“
”的充分不必要條件
②如果命題“
”為假命題，則
中至多有一個為真命題
③設
，若
，則
的最小值為
④函數
在
上存在
，使
，則a的取值范圍
或
.
查看答案和解析>>
科目：高中數學 來源： 題型：
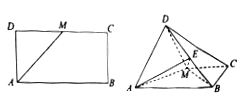
【題目】如圖，已知長方形
中， 
， 
， 
為
的中點.將
沿
折起，使得平面
平面
.
（1）求證： 
；
（2）若點
是線段
上的一動點，問點
在何位置時，二面角
的余弦值為
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在五棱錐
中，平面
平面
，且
．
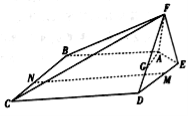
（1）已知點
在線段
上，確定
的位置，使得
平面
；
（2）點
分別在線段
上，若沿直線
將四邊形
向上翻折，
與
恰好重合，求直線
與平面
所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在五棱錐
中，平面
平面
，且
．
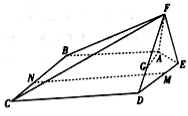
（1）已知點
在線段
上，確定
的位置，使得
平面
；
（2）點
分別在線段
上，若沿直線
將四邊形
向上翻折，
與
恰好重合，求三棱錐
的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某單位共有老、中、青職工430人,其中青年職工160人，中年職工人數是老年職工人數的2倍。為了解職工身體狀況，現采用分層抽樣方法進行調查，在抽取的樣本中有青年職工32人，則該樣本中的老年職工人數為
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
，圓
與
軸交于
兩點，過點
的圓的切線為
是圓上異于的一點，
垂直于軸，垂足為
，
是的中點，延長
分別交
于
．
（1）若點
，求以
為直徑的圓的方程，并判斷
是否在圓上；
（2）當在圓上運動時，證明：直線
恒與圓相切．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在透明塑料制成的長方體
容器內灌進一些水（未滿），現將容器底面一邊
固定在底面上，再將容器傾斜，隨著傾斜度的不同，有下列四種說法：
①水的部分始終呈棱柱狀；
②水面四邊形
的面積為定值；
③棱
始終與水面
平行；
④若
， 
，則
是定值.
則其中正確命題的個數的是（ ）
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com