【題目】已知拋物線的頂點在原點，它的準線過雙曲線 
的右焦點，而且與x軸垂直．又拋物線與此雙曲線交于點 
，求拋物線和雙曲線的方程．
【答案】解：由題意，設拋物線方程為y2=﹣2px（p＞0）
∵拋物線圖象過點 
，∴ 
，解之得p=2．
所以拋物線方程為y2=﹣4x，準線方程為x=1．
∵雙曲線的右焦點經過拋物線的準線，∴雙曲線右焦點坐標為（1，0），c=1
∵雙曲線經過點 ，∴ 
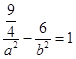
結合c2=a2+b2=1，聯解得 
或a2=9，b2=﹣8（舍去）
∴雙曲線方程為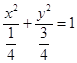 
．
綜上所述，拋物線方程為y2=﹣4x，雙曲線方程為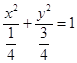
【解析】根據題中的點在拋物線上，列式解出拋物線方程為y2=﹣2x，從而算出雙曲線右焦點坐標為（1，0），可得c2=a2+b2=1．再由點 
在雙曲線上建立關于a、b的方程，聯解得到a、b的值，即可得到雙曲線的方程．
優生樂園系列答案科目：高中數學 來源： 題型：
【題目】已知△ABC的內角A，B，C的對邊分別為a，b，c，若cosA= 
，c=3b，且△ABC面積S△ABC= 
．
（1）求邊b．c；
（2）求邊a并判斷△ABC的形狀．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了檢測某輪胎公司生產的輪胎的寬度，需要抽檢一批輪胎（共10個輪胎），已知這批輪胎寬度（單位： 
）的折線圖如下圖所示：
（1）求這批輪胎寬度的平均值；
（2）現將這批輪胎送去質檢部進行抽檢，抽檢方案是：從這批輪胎中任取5個作檢驗，這5個輪胎的寬度都在
內，則稱這批輪胎合格，如果抽檢不合格，就要重新再抽檢一次，若還是不合格，這批輪胎就認定不合格.
求這批輪胎第一次抽檢就合格的概率；
記
為這批輪胎的抽檢次數，求
的分布列及數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現有8名奧運會志愿者，其中志愿者A1 ， A2 ， A3通曉日語，B1 ， B2 ， B3通曉俄語，C1 ， C2通曉韓語．從中選出通曉日語、俄語和韓語的志愿者各1名，組成一個小組．
（1）求A1被選中的概率；
（2）求B1和C1不全被選中的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設向量 
， 
的夾角為60°且| |=| |=1，如果 
， 
， 
．
（1）證明：A、B、D三點共線．
（2）試確定實數k的值，使k的取值滿足向量 
與向量 
垂直．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P﹣ABCD中，底面ABCD是邊長為1的正方形，側棱PA的長為2，且PA與AB，AD的夾角都等于60°，M是PC的中點，設 
= 
， 
= 
， 
= 
． 
（1）試用 ， ， 表示出向量 
；
（2）求BM的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若（a+b+c）（b+c﹣a）=3ab，且sinA=2sinBcosC，那么△ABC是（ ）
A.直角三角形
B.等邊三角形
C.等腰三角形
D.等腰直角三角形
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC 中，角A，B，C所對的邊分別為a，b，c，且asin Acos C+csin AcosA= 
c
（1）若c=1，sin C= ，求△ABC的面積S
（2）若D 是AC的中點且cosB= 
，BD= 
，求△ABC的最短邊的邊長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=loga（2x+1），g（x）=loga（1﹣2x）（a＞0且a≠1）
（1）求函數F（x）=f（x）﹣g（x）的定義域；
（2）判斷F（x）=f（x）﹣g（x）的奇偶性，并說明理由；
（3）確定x為何值時，有f（x）﹣g（x）＞0．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com