
【題目】棉花的纖維長度是棉花質量的重要指標,在一批棉花中隨機抽測了60根棉花的纖維長度(單位:mm),按從小到大排序結果如下:
25 28 33 50 52 58 59 60 61 62
82 86 113 115 140 143 146 170 175 195
202 206 233 236 238 255 260 263 264 265
293 293 294 296 301 302 303 305 305 306
321 323 325 326 328 340 343 346 348 350
352 355 357 357 358 360 370 380 383 385
(1)請你選擇合適的組距,作出這個樣本的頻率分布直方圖,分析這批棉花纖維長度分布的特征;
(2)請你估計這批棉花的第5,95百分位數.
【答案】(1)直方圖見解析,有一部分棉花的纖維長度比較短,這批棉花中混進了一些次品;(2)41.5,375.
【解析】
(1)可以每60 mm為一組,即直方圖中第小上矩形寬度為60,分組后計算頻率,畫出直方圖,從圖中可看出纖維較短的不少,有次品混入.
(2)計算![]() ,因此取第3項與第4項,第57項與第58項數據的平均數作為相應百分位估計值,
,因此取第3項與第4項,第57項與第58項數據的平均數作為相應百分位估計值,
(1)頻率分布直方圖如圖,由圖分析發現這批棉花的纖維長度不是特別均勻,有一部分棉花的纖維長度比較短,所以,這批棉花中混進了一些次品;

(2)由![]() ,可知樣本數據的第5,95百分位數為第3項與第4項,第57項與第58項數據的平均數,分別為41.5,375.據此可估計這批棉花的第5,95百分位數分別約為41.5,375.
,可知樣本數據的第5,95百分位數為第3項與第4項,第57項與第58項數據的平均數,分別為41.5,375.據此可估計這批棉花的第5,95百分位數分別約為41.5,375.


科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).以平面直角坐標系
為參數).以平面直角坐標系![]() 的原點
的原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,取相同的單位長度建立極坐標系,設直線
軸的正半軸為極軸,取相同的單位長度建立極坐標系,設直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 和直線
和直線![]() 的普通方程;
的普通方程;
(2)設![]() 為曲線
為曲線![]() 上任意一點,求點
上任意一點,求點![]() 到直線
到直線![]() 的距離的最值.
的距離的最值.
【答案】(1)![]() ,
, ![]() ;(2)最大值為
;(2)最大值為![]() ,最小值為
,最小值為![]()
【解析】試題分析:(1)根據參數方程和極坐標化普通方程化法即易得結論![]() 的普通方程為
的普通方程為![]() ;直線
;直線![]() 的普通方程為
的普通方程為![]() .(2)求點到線距離問題可借助參數方程,利用三角函數最值法求解即可故設
.(2)求點到線距離問題可借助參數方程,利用三角函數最值法求解即可故設![]() ,
, ![]()
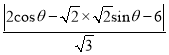
![]()
 .即可得出最值
.即可得出最值
解析:(1)根據題意,由 ,得
,得![]() ,
, ![]() ,
,
由![]() ,得
,得![]() ,
,
故![]() 的普通方程為
的普通方程為![]() ;
;
由![]() 及
及![]() ,
, ![]() 得
得![]() ,
,
故直線![]() 的普通方程為
的普通方程為![]() .
.
(2)由于![]() 為曲線
為曲線![]() 上任意一點,設
上任意一點,設![]() ,
,
由點到直線的距離公式得,點![]() 到直線
到直線![]() 的距離為
的距離為
![]()

![]()
 .
.
∵![]()
![]() ,
,
∴
 ,即
,即![]()
![]() ,
,
故點![]() 到直線
到直線![]() 的距離的最大值為
的距離的最大值為![]() ,最小值為
,最小值為![]() .
.
點睛:首先要熟悉參數方程和極坐標方程化普通方程的方法,第一問基本屬于送分題所以務必抓住,對于第二問可以總結為一類題型,借助參數方程設點的方便轉化為三角函數最值問題求解
【題型】解答題
【結束】
23
【題目】已知函數![]() ,
,![]() .
.
(1)解關于![]() 的不等式
的不等式![]() ;
;
(2)若函數![]() 的圖象恒在函數
的圖象恒在函數![]() 圖象的上方,求
圖象的上方,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業擬用10萬元投資甲、乙兩種商品.已知各投入![]() 萬元,甲、乙兩種商品分別可獲得
萬元,甲、乙兩種商品分別可獲得![]() 萬元的利潤,利潤曲線
萬元的利潤,利潤曲線![]() ,
,![]() ,如圖所示.
,如圖所示.

(1)求函數![]() 的解析式;
的解析式;
(2)應怎樣分配投資資金,才能使投資獲得的利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,點
,點![]() 也為拋物線
也為拋物線![]() 的焦點.(1)若
的焦點.(1)若![]() 為橢圓
為橢圓![]() 上兩點,且線段
上兩點,且線段![]() 的中點為
的中點為![]() ,求直線
,求直線![]() 的斜率;
的斜率;
(2)若過橢圓![]() 的右焦點
的右焦點![]() 作兩條互相垂直的直線分別交橢圓于
作兩條互相垂直的直線分別交橢圓于![]() 和
和![]() ,設線段
,設線段![]() 的長分別為
的長分別為![]() ,證明
,證明![]() 是定值.
是定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率
,離心率![]() ,且橢圓的短軸長為2.
,且橢圓的短軸長為2.
(1)球橢圓的標準方程;
(2)已知直線![]() 過右焦點
過右焦點![]() ,且它們的斜率乘積為
,且它們的斜率乘積為![]() ,設
,設![]() 分別與橢圓交于點
分別與橢圓交于點![]() 和
和![]() .
.
①求![]() 的值;
的值;
②設![]() 的中點
的中點![]() ,
,![]() 的中點為,求
的中點為,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調查某地區老年人是否需要志愿者提供幫助,用簡單隨機抽樣的方法從該地區調查了500位老年人,結果如下:
性別 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附:![]() 的觀測值
的觀測值
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估計該地區老年人中,需要志愿者提供幫助的老年人的比例;
(2)在犯錯誤的概率不超過0.01的前提下是否可認為該地區的老年人是否需要志愿者提供幫助與性別有關?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 年諾貝爾生理學或醫學獎獲得者威廉·凱林(WilliamG.KaelinJr)在研究腎癌的
年諾貝爾生理學或醫學獎獲得者威廉·凱林(WilliamG.KaelinJr)在研究腎癌的![]() 抑制劑過程中使用的輸液瓶可以視為兩個圓柱的組合體.開始輸液時,滴管內勻速滴下液體(滴管內液體忽略不計),設輸液開始后
抑制劑過程中使用的輸液瓶可以視為兩個圓柱的組合體.開始輸液時,滴管內勻速滴下液體(滴管內液體忽略不計),設輸液開始后![]() 分鐘,瓶內液面與進氣管的距離為
分鐘,瓶內液面與進氣管的距離為![]() 厘米,已知當
厘米,已知當![]() 時,
時,![]() .如果瓶內的藥液恰好
.如果瓶內的藥液恰好![]() 分鐘滴完.則函數
分鐘滴完.則函數![]() 的圖像為( )
的圖像為( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司對員工實行新的臨時事假制度:“每位員工每月在正常的工作時間臨時有事,可請假至多三次,每次至多一小時”,現對該制度實施以來![]() 名員工請假的次數進行調查統計,結果如下表所示:
名員工請假的次數進行調查統計,結果如下表所示:
請假次數 |
|
|
|
|
人數 |
|
|
|
|
根據上表信息解答以下問題:
(1)從該公司任選兩名員工,求這兩人請假次數之和恰為![]() 的概率;
的概率;
(2)從該公司任選兩名員工,用![]() 表示這兩人請假次數之差的絕對值,求隨機變量
表示這兩人請假次數之差的絕對值,求隨機變量![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com