
函數(shù)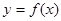 為定義在
為定義在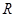 上的減函數(shù),函數(shù)
上的減函數(shù),函數(shù)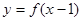 的圖像關(guān)于點(diǎn)(1,0)
的圖像關(guān)于點(diǎn)(1,0)
對稱, 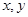 滿足不等式
滿足不等式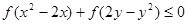 ,
,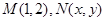 ,
,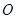 為坐標(biāo)原點(diǎn),則當(dāng)
為坐標(biāo)原點(diǎn),則當(dāng)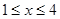 時,
時,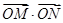 的取值范圍為 ( )
的取值范圍為 ( )
A.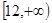 | B.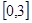 | C.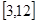 | D.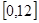 |
D
解析試題分析:判斷函數(shù)的奇偶性,推出不等式,利用約束條件畫出可行域,然后求解數(shù)量積的范圍即可.解:函數(shù)y=f(x-1)的圖象關(guān)于點(diǎn)(1,0)對稱,所以f(x)為 奇函數(shù).∴f(x2-2x)≤f(-2y+y2)≤0,∴x2-2x≥-2y+y2,
x2-2x≥y2-2y, 1≤x≤4畫出可行域如圖,
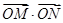 =x+2y∈[0,12].故選D.
=x+2y∈[0,12].故選D.
考點(diǎn):線性規(guī)劃
點(diǎn)評:本題考查函數(shù)的奇偶性,線性規(guī)劃的應(yīng)用,向量的數(shù)量積的知識,是綜合題,考查數(shù)形結(jié)合與計算能力


 小學(xué)教材完全解讀系列答案
小學(xué)教材完全解讀系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:單選題
已知點(diǎn)P的坐標(biāo) ,過點(diǎn)P的直線l與圓
,過點(diǎn)P的直線l與圓 相交于A、B兩點(diǎn),則
相交于A、B兩點(diǎn),則 的最小值為( )
的最小值為( )
A.2 B.4 C. D.
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
在平面直角坐標(biāo)系中,若不等式組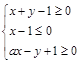 (
(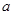 為常數(shù))所表示的平面區(qū)域的面積等于
為常數(shù))所表示的平面區(qū)域的面積等于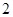 ,則
,則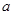 的值為
的值為
| A.-5 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
完成一項(xiàng)裝修工程,木工和瓦工的比例為2∶3,請木工需付日工資每人50元,請瓦工需付日工資每人40元,現(xiàn)有日工資預(yù)算2 000元,設(shè)每天請木工x人、瓦工y人,則每天請木、瓦工人數(shù)的約束條件( )
A.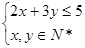 B.
B.
C D.
D.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com