
【題目】已知四棱錐![]() ,底面
,底面![]() 為菱形,
為菱形, ![]() 為
為![]() 上的點,過
上的點,過![]() 的平面分別交
的平面分別交![]() 于點
于點![]() ,且
,且![]() 平面
平面![]() .
.
(1)證明: ![]() ;
;
(2)當![]() 為
為![]() 的中點,
的中點, ![]() ,
, ![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求平面AMHN與平面ABCD所成銳二面角的余弦值.
,求平面AMHN與平面ABCD所成銳二面角的余弦值.
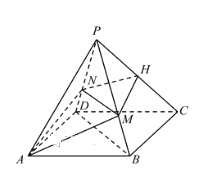
【答案】(1)見解析;(2) ![]() .
.
【解析】試題分析:
(1)連![]() 交
交![]() 于點
于點![]() ,連
,連![]() ,則得
,則得![]() ,進而可得
,進而可得![]() 平面
平面![]() ,于是
,于是![]() .由線面平行的性質可得
.由線面平行的性質可得![]() ,所以得
,所以得![]() .(2)由條件可得
.(2)由條件可得![]() 兩兩垂直,建立空間直角坐標系,然后分別求出平面AMHN與平面ABCD的法向量,通過兩法向量的夾角的余弦值可得所求.
兩兩垂直,建立空間直角坐標系,然后分別求出平面AMHN與平面ABCD的法向量,通過兩法向量的夾角的余弦值可得所求.
試題解析:
(1)證明:連![]() 交
交![]() 于點
于點![]() ,連
,連![]() .
.
因為四邊形![]() 為菱形,
為菱形,
所以![]() ,且
,且![]() 為
為![]() 、
、![]() 的中點.
的中點.
因為![]() ,
,
所以![]() ,
,
又![]() 且
且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
因為![]() 平面
平面![]() ,
,
所以![]() .
.
因為![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() ,
,
所以![]() .
.
(2)由(1)知![]() 且
且![]() ,
,
因為![]() ,且
,且![]() 為
為![]() 的中點,
的中點,
所以![]() ,
,
又![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
所以![]() ,
,
因為![]() ,
,
所以![]() .
.
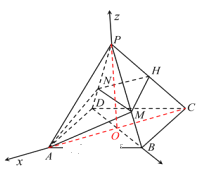
分別以![]() 為
為![]() 軸,建立如圖所示空間直角坐標系
軸,建立如圖所示空間直角坐標系![]() .
.
設![]() ,則
,則![]()
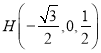 ,
,
所以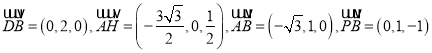
設平面![]() 的法向量為
的法向量為![]() ,
,
則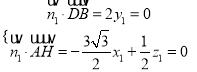 ,令
,令![]() ,得
,得![]() .
.
由題意可得平面![]() 的法向量為
的法向量為![]() ,
,
所以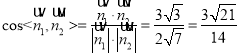 .
.
所以平面AMHN與平面ABCD所成銳二面角的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() ,…,
,…,![]() 是1,2,…,
是1,2,…,![]() 的一個排列,把排在
的一個排列,把排在![]() 的左邊且比
的左邊且比![]() 小的數的個數稱為
小的數的個數稱為![]() 的順序數,如在排列6,4,5,3,2,1中,5的順序數為1,3的順序數為0,則在1至8這8個數的排列中,8的順序數為2,7的順序數為3,5的順序數為3的不同排列的種數為
的順序數,如在排列6,4,5,3,2,1中,5的順序數為1,3的順序數為0,則在1至8這8個數的排列中,8的順序數為2,7的順序數為3,5的順序數為3的不同排列的種數為
A. 96B. 144C. 192D. 240
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱長均相等的四棱錐![]() 中,
中, ![]() 為底面正方形的中心,
為底面正方形的中心, ![]() ,
,![]() 分別為側棱
分別為側棱![]() ,
,![]() 的中點,有下列結論正確的有:( )
的中點,有下列結論正確的有:( )

A.![]() ∥平面
∥平面![]() B.平面
B.平面![]() ∥平面
∥平面![]()
C.直線![]() 與直線
與直線![]() 所成角的大小為
所成角的大小為![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,圖①是棱長為1的小正方體,圖②,③是由這樣的小正方體擺放而成.按照這樣的方法繼續擺放,由上而下分別將第1層,第2層,…,第![]() 層的小正方體的個數記為
層的小正方體的個數記為![]() ,解答下列問題:
,解答下列問題:
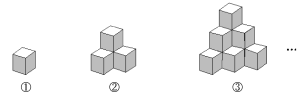
(1)按照要求填表:
| 1 | 2 | 3 | 4 | … |
| 1 | 3 | 6 | _ | … |
(2)![]() __________.
__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙3位大學生同時應聘某個用人單位的職位,甲、乙兩人只有一人被選中的概率為![]() ,兩人都被選中的概率為
,兩人都被選中的概率為![]() ,丙被選中的概率為
,丙被選中的概率為![]() ,且三人各自能否被選中互不影響.
,且三人各自能否被選中互不影響.
(1)求3人同時被選中的概率;
(2)求恰好有2人被選中的概率;
(3)求3人中至少有1人被選中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列兩組數據:甲:12,13,11,10,14.乙:10,17,10,13,10.
(1)分別計算兩組數據的平均差,并根據計算結果判斷哪組數據波動大.
(2)分別計算兩組數據的方差,并根據計算結果判斷哪組數據波動大.
(3)以上兩種判斷方法的結果是否一致?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若一個函數當自變量在不同范圍內取值時,函數表達式不同,我們稱這樣的函數為分段函數.下面我們參照學習函數的過程與方法,探究分段函數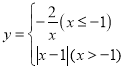 的圖象與性質.列表:
的圖象與性質.列表:
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描點:在平面直角坐標系中,以自變量x的取值為橫坐標,以相應的函數值y為縱坐標,描出相應的點,如圖所示.
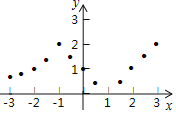
(1)如圖,在平面直角坐標系中,觀察描出的這些點的分布,作出函數圖象;
(2)研究函數并結合圖象與表格,回答下列問題:
①點![]() ,
,![]() ,
,![]() ,
,![]() 在函數圖象上,
在函數圖象上,![]()
![]() ,
,![]()
![]() ;(填“>”,“=”或“<”)
;(填“>”,“=”或“<”)
②當函數值![]() 時,求自變量x的值;
時,求自變量x的值;
③在直線![]() 的右側的函數圖象上有兩個不同的點
的右側的函數圖象上有兩個不同的點![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
④若直線![]() 與函數圖象有三個不同的交點,求a的取值范圍.
與函數圖象有三個不同的交點,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com