
..(本小題滿分12分)如圖,在正方體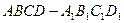 中,
中,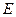 、
、 分別為棱
分別為棱 、
、 的中點.
的中點.
(1)求證: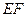 ∥平面
∥平面 ;
;
(2)求證:平面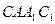 ⊥平面
⊥平面 ;
;
(3)如果 ,一個動點從點
,一個動點從點 出發在正方體的
出發在正方體的
表面上依次經過棱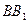 、
、 、
、 、
、 、
、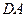 上的點,最終又回到點
上的點,最終又回到點 ,指出整個路線長度的最小值并說明理由.
,指出整個路線長度的最小值并說明理由.
在正方體 中,對角線
中,對角線 .
.
又 E、F為棱AD、AB的中點,
E、F為棱AD、AB的中點,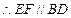 .
. . …………2分
. …………2分
又B1D1平面 ,
, 平面
平面 ,
, EF∥平面CB1D1. …………4分
EF∥平面CB1D1. …………4分
(2)證明: 在正方體
在正方體 中,AA1⊥平面A1B1C1D1,
中,AA1⊥平面A1B1C1D1,
而B1D1平面A1B1C1D1, AA1⊥B1D1.
AA1⊥B1D1.
又 在正方形A1B1C1D1中,A1C1⊥B1D1,
在正方形A1B1C1D1中,A1C1⊥B1D1, B1D1⊥平面CAA1C1. …………6分
B1D1⊥平面CAA1C1. …………6分
又 B1D1平面CB1D1,
B1D1平面CB1D1, 平面CAA1C1⊥平面CB1D1. …………8分
平面CAA1C1⊥平面CB1D1. …………8分
(3)最小值為  . …………9分
. …………9分
如圖,將正方體六個面展開成平面圖形, …………10分
從圖中F到F,兩點之間線段最短,而且依次經過棱BB1、B1C1、C1D1、D1D、DA上的中點,所求的最小值為  . …………12分.
. …………12分.
解析


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| ON |
| ON |
| 5 |
| OM |
| OT |
| M1M |
| N1N |
| OP |
| OA |
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)已知關于![]() 的一元二次函數
的一元二次函數![]() (Ⅰ)設集合P={1,2, 3}和Q={-1,1,2,3,4},分別從集合P和Q中隨機取一個數作為
(Ⅰ)設集合P={1,2, 3}和Q={-1,1,2,3,4},分別從集合P和Q中隨機取一個數作為![]() 和
和![]() ,求函數
,求函數![]() 在區間[
在區間[![]() 上是增函數的概率;(Ⅱ)設點(
上是增函數的概率;(Ⅱ)設點(![]() ,
,![]() )是區域
)是區域 內的隨機點,求函數
內的隨機點,求函數![]() 上是增函數的概率。
上是增函數的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分) 一幾何體![]() 的三視圖如圖所示,
的三視圖如圖所示,![]() ,A1A=
,A1A=![]() ,AB=
,AB=![]() ,AC=2,A1C1=1,
,AC=2,A1C1=1,![]() 在線段
在線段![]() 上且
上且![]() =
=![]() .
.
(I)證明:平面![]() ⊥平面
⊥平面![]() ;
;
(II)求二面角![]() 的余弦值.
的余弦值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com