【題目】已知拋物線
，直線
傾斜角是
且過拋物線
的焦點，直線
被拋物線
截得的線段長是16，雙曲線
： 
的一個焦點在拋物線
的準線上，則直線
與
軸的交點
到雙曲線
的一條漸近線的距離是（ ）
A. 2 B. 
C. 
D. 1
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】在一次抗洪搶險中，準備用射擊的方法引爆從橋上游漂流而下的一個巨大的汽油灌，已知只有5發子彈，第一次命中只能使汽油流出，第二次命中才能引爆．每次射擊相互獨立，且命中概率都是
，求（1）油罐被引爆的概率；（2）如果引爆或子彈打光則停止射擊，設射擊次數為
，求
的分布列．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列命題：①定義在
上的函數
滿足
，則
一定不是
上的減函數；
②用反證法證明命題“若實數
，滿足
，則
都為0”時，“假設命題的結論不成立”的敘述是“假設
都不為0”；
③把函數
的圖象向右平移
個單位長度，所得到的圖象的函數解析式為
；
④“
”是“函數
為奇函數”的充分不必要條件.
其中所有正確命題的序號為__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
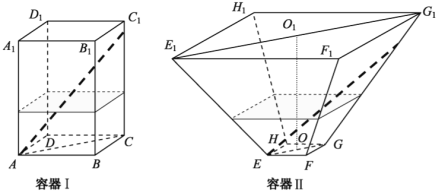
【題目】如圖，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱臺形玻璃容器Ⅱ的高均為32cm，容器Ⅰ的底面對角線AC的長為10
cm，容器Ⅱ的兩底面對角線
，
的長分別為14cm和62cm．分別在容器Ⅰ和容器Ⅱ中注入水，水深均為12cm．現有一根玻璃棒l，其長度為40cm．（容器厚度、玻璃棒粗細均忽略不計）
（1）將
放在容器Ⅰ中，的一端置于點A處，另一端置于側棱
上，求沒入水中部分的長度；
（2）將放在容器Ⅱ中，的一端置于點E處，另一端置于側棱
上，求沒入水中部分的長度．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知四棱錐
的底面為矩形，D為
的中點，AC⊥平面BCC1B1．
（Ⅰ）證明：AB//平面CDB1;
（Ⅱ）若AC=BC=1，BB1=
,
（1）求BD的長；
（2）求B1D與平面ABB1所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
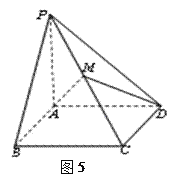
【題目】如圖5所示，已知四棱錐
中，底面
為矩形， 
底面
， 
，
， 
為
的中點.
⑴指出平面
與
的交點
所在位置，并給出理由；
⑵求平面
將四棱錐
分成上下兩部分的體積比.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】天氣預報是氣象專家根據預測的氣象資料和專家們的實際經驗，經過分析推斷得到的，在現實的生產生活中有著重要的意義，某快餐企業的營銷部門對數據分析發現，企業經營情況與降雨填上和降雨量的大小有關.
（1）天氣預報所，在今后的三天中，每一天降雨的概率為40%，該營銷部分通過設計模擬實驗的方法研究三天中恰有兩天降雨的概率，利用計算機產生0大9之間取整數值的隨機數，并用
表示下雨，其余
個數字表示不下雨，產生了20組隨機數：
求由隨機模擬的方法得到的概率值；
（2）經過數據分析，一天內降雨量的大小
（單位：毫米）與其出售的快餐份數
成線性相關關系，該營銷部門統計了降雨量與出售的快餐份數的數據如下：
試建立
關于
的回歸方程，為盡量滿足顧客要求又不在造成過多浪費，預測降雨量為6毫米時需要準備的快餐份數.（結果四舍五入保留整數）
附注：回歸方程
中斜率和截距的最小二乘法估計公式分別為：
， 
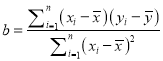查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
