設(shè)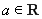 ,函數(shù)
,函數(shù)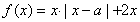 .
.
(1)若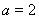 ,求函數(shù)
,求函數(shù)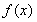 在區(qū)間
在區(qū)間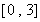 上的最大值;
上的最大值;
(2)若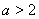 ,寫出函數(shù)
,寫出函數(shù)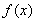 的單調(diào)區(qū)間(不必證明);
的單調(diào)區(qū)間(不必證明);
(3)若存在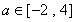 ,使得關(guān)于
,使得關(guān)于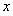 的方程
的方程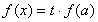 有三個不相等的實數(shù)解,求實數(shù)
有三個不相等的實數(shù)解,求實數(shù)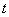 的取值范圍.
的取值范圍.
(1)9(2)單調(diào)遞增區(qū)間是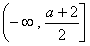 和
和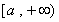 ,單調(diào)遞減區(qū)間是
,單調(diào)遞減區(qū)間是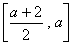 (3)
(3)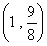
【解析】(1)當(dāng)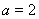 ,
,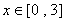 時,
時,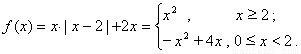

作函數(shù)圖像(圖像略),可知函數(shù)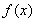 在區(qū)間
在區(qū)間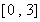 上是增函數(shù),所以
上是增函數(shù),所以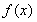 的最大值為
的最大值為 .…………(4分)
.…………(4分)
(2)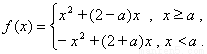 ……(1分)
……(1分)
①當(dāng)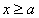 時,
時, ,
,
因為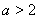 ,所以
,所以 ,
,
所以 在
在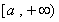 上單調(diào)遞增.…………(3分)
上單調(diào)遞增.…………(3分)
②當(dāng)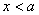 時,
時, ,
,
因為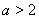 ,所以
,所以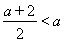 ,所以
,所以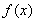 在
在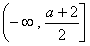 上單調(diào)遞增,在
上單調(diào)遞增,在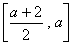 上單調(diào)遞減.…………(5分)
上單調(diào)遞減.…………(5分)
綜上,函數(shù)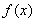 的單調(diào)遞增區(qū)間是
的單調(diào)遞增區(qū)間是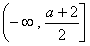 和
和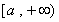 ,
,
單調(diào)遞減區(qū)間是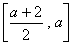 .………………(6分)
.………………(6分)
(3)①當(dāng)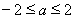 時,
時,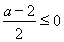 ,
,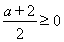 ,所以
,所以 在
在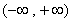 上是增函數(shù),關(guān)于
上是增函數(shù),關(guān)于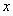 的方程
的方程 不可能有三個不相等的實數(shù)解.…………(2分)
不可能有三個不相等的實數(shù)解.…………(2分)
②當(dāng) 時,由(1)知
時,由(1)知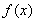 在
在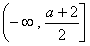 和
和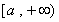 上分別是增函數(shù),在
上分別是增函數(shù),在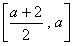 上是減函數(shù),當(dāng)且僅當(dāng)
上是減函數(shù),當(dāng)且僅當(dāng) 時,方程
時,方程 有三個不相等的實數(shù)解.
有三個不相等的實數(shù)解.
即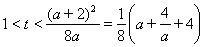 .…………(5分)
.…………(5分)
令 ,
,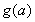 在
在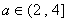 時是增函數(shù),故
時是增函數(shù),故 .…………(7分)
.…………(7分)
所以,實數(shù)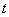 的取值范圍是
的取值范圍是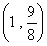 .…………(8分)
.…………(8分)


科目:高中數(shù)學(xué) 來源:2014年高考數(shù)學(xué)全程總復(fù)習(xí)課時提升作業(yè)七十五選修4-2第二節(jié)練習(xí)卷(解析版) 題型:解答題
求矩陣A=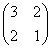 的逆矩陣.
的逆矩陣.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014年高考數(shù)學(xué)全程總復(fù)習(xí)課時提升作業(yè)七十七選修4-4第一節(jié)練習(xí)卷(解析版) 題型:解答題
已知圓O1和圓O2的極坐標(biāo)方程分別為ρ=2,ρ2-2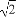 ρcos(θ-
ρcos(θ- )=2.
)=2.
(1)把圓O1和圓O2的極坐標(biāo)方程化為直角坐標(biāo)方程.
(2)求經(jīng)過兩圓交點的直線的極坐標(biāo)方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014年高考數(shù)學(xué)全程總復(fù)習(xí)課時提升作業(yè)七十一第十章第八節(jié)練習(xí)卷(解析版) 題型:選擇題
設(shè)某項試驗的成功率是失敗率的2倍,用隨機(jī)變量X去描述1次試驗的成功次數(shù),則P(X=0)等于( )
(A)0 (B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014年高中數(shù)學(xué)全國各省市理科導(dǎo)數(shù)精選22道大題練習(xí)卷(解析版) 題型:解答題
已知函數(shù)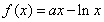 ,
,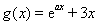 ,其中
,其中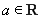 .
.
(Ⅰ)求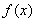 的極值;
的極值;
(Ⅱ)若存在區(qū)間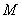 ,使
,使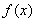 和
和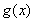 在區(qū)間
在區(qū)間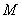 上具有相同的單調(diào)性,求
上具有相同的單調(diào)性,求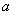 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014年高中數(shù)學(xué)全國各省市理科導(dǎo)數(shù)精選22道大題練習(xí)卷(解析版) 題型:解答題
若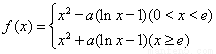 ,其中
,其中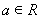 .
.
(1)當(dāng)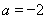 時,求函數(shù)
時,求函數(shù)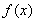 在區(qū)間
在區(qū)間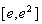 上的最大值;
上的最大值;
(2)當(dāng)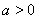 時,若
時,若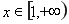 ,
,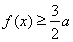 恒成立,求
恒成立,求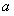 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014年高中數(shù)學(xué)全國各省市理科導(dǎo)數(shù)精選22道大題練習(xí)卷(解析版) 題型:解答題
已知二次函數(shù)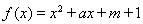 ,關(guān)于x的不等式
,關(guān)于x的不等式 的解集為
的解集為 ,其中m為非零常數(shù).設(shè)
,其中m為非零常數(shù).設(shè)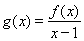 .
.
(1)求a的值;
(2)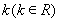 如何取值時,函數(shù)
如何取值時,函數(shù)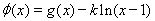 存在極值點,并求出極值點;
存在極值點,并求出極值點;
(3)若m=1,且x>0,求證: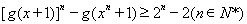
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2014年陜西省咸陽市高考模擬考試(一)理科數(shù)學(xué)試卷(解析版) 題型:選擇題
某幾何體的三視圖如右圖(其中側(cè)視圖中的圓弧是半圓),則該幾何體的表面積為( )
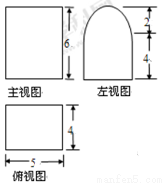
A.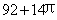 B.
B.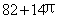 C.
C.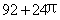 D.
D.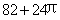
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com