
【題目】已知函數![]()
(1)若函數![]() 有零點,求實數
有零點,求實數![]() 的取值范圍;
的取值范圍;
(2)證明:當![]() 時,
時, ![]()
【答案】(I)![]() ;(II)詳見解析.
;(II)詳見解析.
【解析】試題分析:(I)對函數求導,可得函數單調性,并求得函數的最小值,若函數有零點,函數最小值小于零且在定義域范圍有函數值大于零,解不等式可得![]() 的范圍;(Ⅱ)將
的范圍;(Ⅱ)將![]() 代入不等式化簡為
代入不等式化簡為![]() ,可構造函數
,可構造函數![]()
![]() 利用導數判斷單調性可知在
利用導數判斷單調性可知在![]() 條件下
條件下![]() 最小值為
最小值為![]() ,
, ![]() 最大值為
最大值為![]() .可證命題.
.可證命題.
試題解析:
(Ⅰ)法1: 函數![]() 的定義域為
的定義域為![]() .
.
由![]() , 得
, 得![]() .
.
因為![]() ,則
,則![]() 時,
時, ![]() ;
; ![]() 時,
時, ![]() .
.
所以函數![]() 在
在![]() 上單調遞減, 在
上單調遞減, 在![]() 上單調遞增.
上單調遞增.
當![]() 時,
時, ![]() .
.
當![]() 時, 又
時, 又![]() , 則函數
, 則函數![]() 有零點.
有零點.
所以實數![]() 的取值范圍為
的取值范圍為![]() .
.
法2:函數![]() 的定義域為
的定義域為![]() .
.
由![]() , 得
, 得![]() .
.
令![]() ,則
,則![]() .
.
當![]() 時,
時, ![]() ; 當
; 當![]() 時,
時, ![]() .
.
所以函數![]() 在
在![]() 上單調遞增, 在
上單調遞增, 在![]() 上單調遞減.
上單調遞減.
故![]() 時, 函數
時, 函數![]() 取得最大值
取得最大值![]() .
.
因而函數![]() 有零點, 則
有零點, 則![]() .
.
所以實數![]() 的取值范圍為
的取值范圍為![]() .
.
(Ⅱ) 要證明當![]() 時,
時, ![]() ,
,
即證明當![]() 時,
時, ![]() , 即
, 即![]() .
.
令![]() , 則
, 則![]() .
.
當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
所以函數![]() 在
在![]() 上單調遞減, 在
上單調遞減, 在![]() 上單調遞增.
上單調遞增.
當![]() 時,
時, ![]() .
.
于是,當![]() 時,
時, ![]() ①
①
令![]() , 則
, 則![]() .
.
當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
所以函數![]()
![]() 上單調遞增, 在
上單調遞增, 在![]() 上單調遞減.
上單調遞減.
當![]() 時,
時, ![]() .
.
于是, 當![]() 時,
時, ![]() ②
②
顯然, 不等式①、②中的等號不能同時成立.
故當![]() 時,
時, ![]() .
.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:
【題目】交強險是車主必須為機動車購買的險種,若普通6座以下私家車投保交強險第一年的費用(基準保費)統一為![]() 元,在下一年續保時,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系,發生交通事故的次數越多,費率也就是越高,具體浮動情況如下表:
元,在下一年續保時,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系,發生交通事故的次數越多,費率也就是越高,具體浮動情況如下表:
交強險浮動因素和浮動費率比率表 | ||
浮動因素 | 浮動比率 | |
| 上一個年度未發生有責任道路交通事故 | 下浮10% |
| 上兩個年度未發生有責任道路交通事故 | 下浮20% |
| 上三個及以上年度未發生有責任道路交通事故 | 下浮30% |
| 上一個年度發生一次有責任不涉及死亡的道路交通事故 | 0% |
| 上一個年度發生兩次及兩次以上有責任道路交通事故 | 上浮10% |
| 上一個年度發生有責任道路交通死亡事故 | 上浮30% |
某機構為了 某一品牌普通6座以下私家車的投保情況,隨機抽取了60輛車齡已滿三年的該品牌同型號私家車的下一年續保時的情況,統計得到了下面的表格:
類型 |
|
|
|
|
|
|
數量 | 10 | 5 | 5 | 20 | 15 | 5 |
以這60輛該品牌車的投保類型的頻率代替一輛車投保類型的概率,完成下列問題:
(1)按照我國《機動車交通事故責任強制保險條例》汽車交強險價格的規定, ![]() ,記
,記![]() 為某同學家的一輛該品牌車在第四年續保時的費用,求
為某同學家的一輛該品牌車在第四年續保時的費用,求![]() 的分布列與數學期望;(數學期望值保留到個位數字)
的分布列與數學期望;(數學期望值保留到個位數字)
(2)某二手車銷售商專門銷售這一品牌的二手車,且將下一年的交強險保費高于基本保費的車輛記為事故車,假設購進一輛事故車虧損5000元,一輛非事故車盈利10000元:
①若該銷售商購進三輛(車齡已滿三年)該品牌二手車,求這三輛車中至多有一輛事故車的概率;
②若該銷售商一次購進100輛(車齡已滿三年)該品牌二手車,求他獲得利潤的期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年1月1日,作為貴陽市打造“千園之城”27個示范性公園之一的泉湖公園正式開園.元旦期間,為了活躍氣氛,主辦方設置了水上挑戰項目向全體市民開放.現從到公園游覽的市民中隨機抽取了60名男生和40名女生共100人進行調查,統計出100名市民中愿意接受挑戰和不愿意接受挑戰的男女生比例情況,具體數據如圖表:
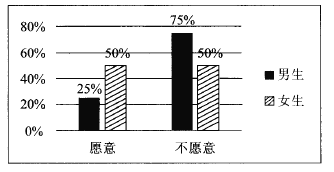
(1)根據條件完成下列![]()
列聯表,并判斷是否在犯錯誤的概率不超過1%的情況下愿意接受挑戰與性別有關?
愿意 | 不愿意 | 總計 | |
男生 | |||
女生 | |||
總計 |
(2)水上挑戰項目共有兩關,主辦方規定:挑戰過程依次進行,每一關都有兩次機會挑戰,通過第一關后才有資格參與第二關的挑戰,若甲參加每一關的每一次挑戰通過的概率均為![]()
,記甲通過的關數為![]()
,求![]()
的分布列和數學期望.
參考公式與數據:
| 0.1 | 0.05 | 0.025 | 0.01 |
| 2.706 | 3.841 | 5.024 | 6.635 |
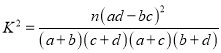
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一醫用放射性物質原來質量為a,每年衰減的百分比相同,當衰減一半時,所用時間是10年,根據需要,放射性物質至少要保留原來的,否則需要更換.已知到今年為止,剩余的為原來的![]() ,
,
(1)求每年衰減的百分比;
(2)到今年為止,該放射性物質已衰減了多少年?
(3)今后至多還能用多少年?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若一數集的任一元素的倒數仍在該集合中,則稱該數集為“可倒數集”.
(1)判斷集合A={-1,1,2}是否為可倒數集;
(2)試寫出一個含3個元素的可倒數集.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:極坐標與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為:
的參數方程為: 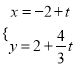 (t為參數),它與曲線C:
(t為參數),它與曲線C: ![]() 相交于A,B兩點.
相交于A,B兩點.
(1)求|AB|的長;
(2)在以O為極點,x軸的正半軸為極軸建立極坐標系,設點P的極坐標為![]() ,求點P到線段AB中點M的距離.
,求點P到線段AB中點M的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將圓![]() 上每一點的縱坐標不變,橫坐標變為原來的
上每一點的縱坐標不變,橫坐標變為原來的![]() ,得曲線C.
,得曲線C.
(Ⅰ)寫出C的參數方程;
(Ⅱ)設直線l: ![]() 與C的交點為P1,P2,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段P1 P2的中點且與l垂直的直線的極坐標方程.
與C的交點為P1,P2,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段P1 P2的中點且與l垂直的直線的極坐標方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com