
【題目】已知函數f(x)=|x﹣a|+m|x+a|.
(1)當m=a=﹣1時,求不等式f(x)≥x的解集;
(2)不等式f(x)≥2(0<m<1)恒成立時,實數a的取值范圍是{a|a≤﹣3或a≥3},求實數m的集合.
【答案】
(1)解:m=a=﹣1時,|x+1|﹣|x﹣1|≥x,
x<﹣1時,﹣(x+1)+(x﹣1)≥x,解得:x≤﹣2,
﹣1≤x≤1時,(x+1)+(x﹣1)≥x,解得:0≤x<1,
x≥1時,(x+1)﹣(x﹣1)≥x,解得:1≤x≤2,
綜上,不等式的解集是{x|x≤﹣2或0≤x≤2};
(2)解:f(x)=|x﹣a|+m|x+a|=m(|x﹣a|+|x+a|)+(1﹣m)|x﹣a|≥2m|a|+(1﹣m)|x﹣a|≥2m|a|≥2,
解得:a≤﹣ ![]() 或a≥
或a≥ ![]() ,
,
∵數a的取值范圍是{a|a≤﹣3或a≥3},
故 ![]() =3,解得:m=
=3,解得:m= ![]() ,
,
∴實數m的集合是{m|m= ![]() }
}
【解析】(1)將m=a=﹣1代入(x),通過討論x的范圍求出不等式的解集即可;(2)根據絕對值的性質得到2m|a|≥2,解出a,得到關于m的方程,解出即可.
【考點精析】關于本題考查的絕對值不等式的解法,需要了解含絕對值不等式的解法:定義法、平方法、同解變形法,其同解定理有;規律:關鍵是去掉絕對值的符號才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】以坐標原點為極點,x軸的正半軸為極軸的極坐標系中,曲線C1的極坐標方程為ρ=2sinθ,正方形ABCD的頂點都在C1上,且依次按逆時針方向排列,點A的極坐標為( ![]() ,
, ![]() ).
).
(1)求點C的直角坐標;
(2)若點P在曲線C2:x2+y2=4上運動,求|PB|2+|PC|2的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正四棱錐P﹣ABCD中,底面ABCD的邊長為4,PD=4,E為PA的中點, 
(1)求證:平面EBD⊥平面PAC;
(2)求直線BE與平面PBD所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲罐中有![]() 個紅球,
個紅球,![]() 個白球和
個白球和![]() 個黑球,乙罐中有
個黑球,乙罐中有![]() 個紅球,
個紅球,![]() 個白球和
個白球和![]() 個黑球。先從甲罐中隨機取出一球放入乙罐,分別以
個黑球。先從甲罐中隨機取出一球放入乙罐,分別以![]() 和
和![]() 表示由甲罐取出的球是紅球,白球和黑球的事件;再從乙罐中隨機取出一球,以
表示由甲罐取出的球是紅球,白球和黑球的事件;再從乙罐中隨機取出一球,以![]() 表示由乙罐取出的球是紅球的事件,則下列結論中正確的是________(寫出所有正確結論的編號)。
表示由乙罐取出的球是紅球的事件,則下列結論中正確的是________(寫出所有正確結論的編號)。
①![]() ; ② 事件
; ② 事件![]() 與事件
與事件![]() 相互獨立;③
相互獨立;③![]()
④![]() 是兩兩互斥的事件;
是兩兩互斥的事件;
⑤![]() 的值不能確定,因為它與
的值不能確定,因為它與![]() 中哪一個發生有關
中哪一個發生有關
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0.現給出如下結論:
①f(0)f(1)>0; ②f(0)f(1)<0;
③f(0)f(3)>0; ④f(0)f(3)<0.
其中正確結論的序號是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+bx+c(a≠0),滿足f(0)=2,f(x+1)﹣f(x)=2x﹣1
(1)求函數f(x)的解析式;
(2)當x∈[﹣1,2]時,求函數的最大值和最小值.
(3)若函數g(x)=f(x)﹣mx的兩個零點分別在區間(﹣1,2)和(2,4)內,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一個水輪的半徑為4米,水輪圓心![]() 距離水面2米,已知水輪每分鐘逆時針轉動4圈,如果當水輪上點
距離水面2米,已知水輪每分鐘逆時針轉動4圈,如果當水輪上點![]() 從水中浮現(圖中點
從水中浮現(圖中點![]() )開始計算時間.
)開始計算時間.
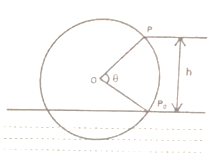
(1)將點![]() 距離水面的高度
距離水面的高度![]() (米)表示為時間
(米)表示為時間![]() (秒)的函數;
(秒)的函數;
(2)在水輪旋轉一圈內,有多長時間點![]() 離開水面?
離開水面?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐![]() (圖1)的三視圖如圖2所示,
(圖1)的三視圖如圖2所示,![]() 為正三角形,
為正三角形,![]() 垂直底面
垂直底面![]() ,俯視圖是直角梯形.
,俯視圖是直角梯形.


圖1 圖2
(1)求正視圖的面積;
(2)求四棱錐![]() 的體積;
的體積;
(3)求證:![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,以O為極點,x軸正半軸為極軸建立極坐標系.曲線C的參數方程為 ![]() (為參數,且0≤<2π),曲線l的極坐標方程為ρ=
(為參數,且0≤<2π),曲線l的極坐標方程為ρ= ![]() (k是常數,且k∈R).
(k是常數,且k∈R).
(1)求曲線C的普通方程和曲線l直角坐標方程;
(2)若曲線l被曲線C截的弦是以( ![]() ,1)為中點,求k的值.
,1)為中點,求k的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com