
【題目】已知橢圓![]() ,傾斜角為
,傾斜角為![]() 的直線與橢圓相交于
的直線與橢圓相交于![]() 兩點,且線段
兩點,且線段![]() 的中點為
的中點為![]() .過橢圓
.過橢圓![]() 內一點
內一點![]() 的兩條直線分別與橢圓交于點
的兩條直線分別與橢圓交于點![]() ,且滿足
,且滿足![]() ,其中
,其中![]() 為實數.當直線
為實數.當直線![]() 平行于
平行于![]() 軸時,對應的
軸時,對應的![]() .
.
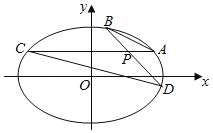
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)當![]() 變化時,
變化時,![]() 是否為定值?若是,請求出此定值;若不是,請說明理由.
是否為定值?若是,請求出此定值;若不是,請說明理由.
【答案】(Ⅰ)![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】
(Ⅰ)將M和N點坐標代入橢圓方程,根據斜率公式求得kMN=1,求得a和b的關系,當直線AP平行于x軸時,設|AC|=2d,求得A點坐標,代入橢圓方程,即可求得a和b,求得橢圓方程;
(Ⅱ)設出A、B、C和D點坐標,由向量共線,![]() =λ
=λ![]() ,
,![]() =λ
=λ![]() ,及A和B在橢圓上,利用斜率公式,kAB=kCD,求得3(1+λ)kAB=﹣2(1+λ),即可求得kAB為定值.
,及A和B在橢圓上,利用斜率公式,kAB=kCD,求得3(1+λ)kAB=﹣2(1+λ),即可求得kAB為定值.
(Ⅰ)設M(m1,n1)、N(m2,n2),則 ,
,
兩式相減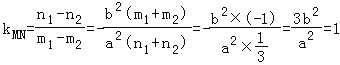 ,
,
故a2=3b2
當直線AP平行于x軸時,設|AC|=2d,
∵![]() ,
,![]() ,則
,則![]() ,解得
,解得![]() ,
,
故點A(或C)的坐標為![]() .
.
代入橢圓方程![]() ,得
,得![]()
a2=3,b2=1,
所以方程為![]() .
.
(Ⅱ)設A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4)
由于![]() ,可得A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),
,可得A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),
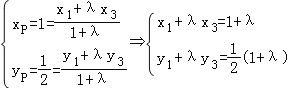 …①
…①
同理![]() 可得
可得 …②
…②
由①②得: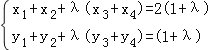 …③
…③
將點A、B的坐標代入橢圓方程得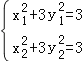 ,
,
兩式相減得(x1+x2)(x1﹣x2)+3(y1+y2)(y1﹣y2)=0,
于是3(y1+y2)kAB=﹣(x1+x2)…④
同理可得:3(y3+y4)kCD=﹣(x3+x4),
于是3(y3+y4)kAB=﹣(x3+x4)(∵AB∥CD,∴kAB=kCD)
所以3λ(y3+y4)kAB=﹣λ(x3+x4)…⑤
由④⑤兩式相加得到:3[y1+y2+λ(y3+y4)]kAB=﹣[(x1+x2)+λ(x3+x4)]
把③代入上式得3(1+λ)kAB=﹣2(1+λ),
解得:![]() ,
,
當λ變化時,kAB為定值,![]() .
.


 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的焦距為
的焦距為![]() ,離心率為
,離心率為![]() ,橢圓的右頂點為
,橢圓的右頂點為![]() .
.
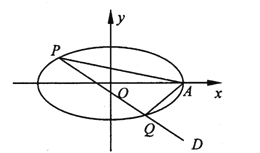
(1)求該橢圓的方程;
(2)過點![]() 作直線
作直線![]() 交橢圓于兩個不同點
交橢圓于兩個不同點![]() ,求證:直線
,求證:直線![]() 的斜率之和為定值.
的斜率之和為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)解不等式![]() ;
;
(2)若函數![]() 在區間
在區間![]() 上存在零點,求實數
上存在零點,求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() ,其中
,其中![]() 為奇函數,
為奇函數,![]() 為偶函數,若不等式
為偶函數,若不等式![]() 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代一部重要的數學著作,書中有如下問題:“今有良馬與駑馬發長安,至齊.齊去長安三千里,良馬初日行一百九十三里,日增一十三里,駑馬初日行九十七里,日減半里.良馬先至齊,復還迎駑馬,問幾何日相逢.”其大意為:“現在有良馬和駑馬同時從長安出發到齊去,已知長安和齊的距離是3000里,良馬第一天行193里,之后每天比前一天多行13里,駑馬第一天行97里,之后每天比前一天少行0.5里.良馬到齊后,立刻返回去迎駑馬,多少天后兩馬相遇.”試確定離開長安后的第天,兩馬相逢.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設關于x的方程x2﹣ax﹣1=0和x2﹣x﹣2a=0的實根分別為x1、x2和x3、x4 , 若x1<x3<x2<x4 , 則實數a的取值范圍為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,斜三棱柱ABC﹣A1B1C1的側面AA1C1C是菱形,側面ABB1A1⊥側面AA1C1C,A1B=AB=AA1=2,△AA1C1的面積為 ![]() ,且∠AA1C1為銳角.
,且∠AA1C1為銳角.
(I) 求證:AA1⊥BC1;
(Ⅱ)求銳二面角B﹣AC﹣C1的余弦值.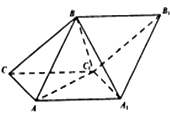
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD﹣A1B1C1D1中,點Q為對角面A1BCD1內一動點,點M、N分別在直線AD和AC上自由滑動,直線DQ與MN所成角的最小值為θ,則下列結論中正確的是( )
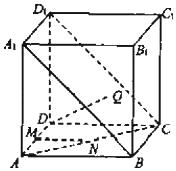
A. 若θ=15°,則點Q的軌跡為橢圓的一部分
B. 若θ=30°,則點Q的軌跡為橢圓的一部分
C. 若θ=45°,則點Q的軌跡為橢圓的一部分
D. 若θ=60°,則點Q的軌跡為橢圓的一部分
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com