設數列{a
n}是等差數列,數列{b
n}是各項都為正數的等比數列,且a
1=b
1=1,b
1+b
2=a
2,b
3是a
1與a
4的等差中項.
(I)求數列{a
n},{b
n}的通項公式;
(II)求數列{
}的前n項和S
n.
分析:(Ⅰ)設{a
n}的公差為d,{b
n}的公比為q,由題設條件知
,由此能求出數列{a
n},{b
n}的通項公式.
(Ⅱ)由a
n=2n-1,
bn=2n-1,知
=
,故S
n=
+
+
+…+
,由此利用錯位相減法能夠求出數列{
}的前n項和S
n.
解答:解:(Ⅰ)∵{a
n}是等差數列,數列{b
n}是各項都為正數的等比數列,
且a
1=b
1=1,b
1+b
2=a
2,b
3是a
1與a
4的等差中項.
設{a
n}的公差為d,{b
n}的公比為q,
∴
,解得d=q=2,或d=q=-
(舍),
∴a
n=1+2(n-1)=2n-1
b
n=2
n-1.
(Ⅱ)∵a
n=2n-1,
bn=2n-1,
∴
=
,
∴S
n=
+
+
+…+
,①
∴
Sn=
+
+
+…+
,②
∴
Sn=1+
+
+
+…+
-
=1+2×
-
=1+2-
-
,
∴S
n=6-
-
.
點評:本題考查數列的通項公式和數列的前n項和公式的求法,解題時要認真審題,注意錯位相減法的合理運用.
練習冊系列答案
相關習題
科目:高中數學
來源:
題型:
(2012•棗莊一模)設數列{a
n}滿足a
1=1,a
2=2,對任意的n∈N
*,a
n+2是a
n+1與a
n的等差中項.
(1)設b
n=a
n+1-a
n,證明數列{b
n}是等比數列,并求出其通項公式;
(2)寫出數列{a
n}的通項公式(不要求計算過程),令
cn=n(-an),求數列{c
n}的前n項和S
n.
查看答案和解析>>
科目:高中數學
來源:2012-2013學年四川省成都市望子成龍學校高二(上)期中數學試卷(解析版)
題型:解答題
設數列{a
n}是等差數列,數列{b
n}是各項都為正數的等比數列,且a
1=b
1=1,b
1+b
2=a
2,b
3是a
1與a
4的等差中項.
(I)求數列{a
n},{b
n}的通項公式;
(II)求數列{
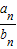
}的前n項和S
n.
查看答案和解析>>
科目:高中數學
來源:2012-2013學年山東省臨沂市重點高中高二(上)期末數學試卷(理科)(解析版)
題型:解答題
設數列{a
n}是等差數列,數列{b
n}是各項都為正數的等比數列,且a
1=b
1=1,b
1+b
2=a
2,b
3是a
1與a
4的等差中項.
(I)求數列{a
n},{b
n}的通項公式;
(II)求數列{
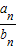
}的前n項和S
n.
查看答案和解析>>
科目:高中數學
來源:2012-2013學年四川省成都市望子成龍學校高二(上)期中數學試卷(解析版)
題型:解答題
設數列{a
n}是等差數列,數列{b
n}是各項都為正數的等比數列,且a
1=b
1=1,b
1+b
2=a
2,b
3是a
1與a
4的等差中項.
(I)求數列{a
n},{b
n}的通項公式;
(II)求數列{
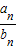
}的前n項和S
n.
查看答案和解析>>



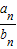 }的前n項和Sn.
}的前n項和Sn.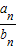 }的前n項和Sn.
}的前n項和Sn.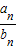 }的前n項和Sn.
}的前n項和Sn.